Kezdőlap


Feladat:	832. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Boldizsár Ferenc , Lux Judit
Füzet:	1964/február, 66 - 68. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Középvonal, Kör (és részhalmaza), mint mértani hely, Paralelogrammák, Diszkusszió, Négyszögek szerkesztése, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/március: 832. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett $A B C D$ négyszögben az $A B$ , $B C$ , $C D$ , $D A$ oldal felezőpontja rendre $K$ , $L$ , $M$ , $N$ és $A B = a$ , $C D = c$ , $A C = e$ , $K M = g$ , $L N = h$ , ahol $a$ , $c$ , $e$ , $g$ , $h$ rendre az adott szakaszok. ‐ Ismeretes egyrészt, hogy a $K L M N$ négyszög paralelogramma; középpontját ( $K M$ és $L N$ metszéspontját) jelöljük $O$ -val. Másrészt $M N$ az $A C D$ háromszög középvonala, tehát fele akkora, mint az $A C$ átló. ‐ Az $A$ csúcs egyrészt a $K$ körül $a / 2$ sugárral írt $k_{1}$ körön van, másrészt ‐ mint $D$ -nek $N$ -re vett tükörképe ‐ $D$ mértani helyének, az $M$ körül $c / 2$ sugárral írt $k_{2}$ körnek $N$ -re vett $k_{3}$ tükörképén. $k_{3}$ középpontját $M'$ -vel jelölve $M M' = 2 M N = C A = e$ , és $N O$ a $K M M'$ háromszög középvonala, tehát 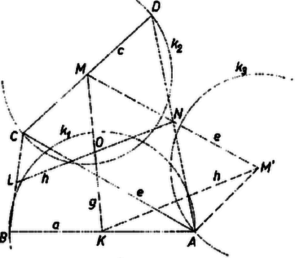$K M' = 2 N O = N L = h$ .

Ezek szerint a szerkesztés a következőképpen végezhető: az

e

g

h

szakaszokból

K M' M

háromszöget szerkesztünk úgy, hogy

M' M = e

M K = g

K M' = h

; az

M M'

oldal felezőpontja legyen

N

. A

K

körül

a / 2

és

M'

körül

c / 2

sugárral írt körök metszéspontja

A

, ennek tükörképe

K

-ra és

N

-re

B

, ill.

D

, végül

D

tükörképe

M

-re

C

.
Az

A B C D

négyszög megfelel a feladat követelményeinek. Ugyanis a szerkesztés folytán

A B = a

C M

A M'

szakasz kétszeri tükrözésével keletkezett, tehát egyenlő és egyirányúan párhuzamos

A M'

-vel, ezért az

A M' M C

négyszög paralelogramma, és egyrészt

A C = M M' = e

, másrészt

C D = 2 C M = 2 A M' = c

. Ekkor

K

N

M

B A D C

négyszög három egymás utáni oldalának felezőpontja, és

K M = g

. Messe végül a

K

-n át

M N

-nel húzott párhuzamos

B C

-t

L

-ben. Ez felezi

B C

-t, mert

K L

A B C

háromszög

A C

-vel párhuzamos középvonala. Továbbá

K L = A C / 2 = N M

, a

K L M N

négyszög paralelogramma,

K M

és

L N

átlói felezik egymást egy

O

pontban, ezért egyrészt

N L = 2 N O

, másrészt

N O

K M' M

háromszög középvonala,

K M' = 2 N O

, tehát

N L = K M' = h

.
A

K M' M

háromszög és

N

egyértelműen létrejön, ha az

e

g

h

szakaszok eleget tesznek a háromszög-egyenlőtlenségnek:

| g - h | < e < g + h

‐, egyenlőség nem állhat, mert egy egyenesen fekvő

K

N

M

felezőpont‐hármasra vezetne.

A

létrejön, ha a

h

a / 2

c / 2

szakaszokból háromszög szerkeszthető, itt elfajulást is megengedhetünk, a megoldások száma 2, ill. 1, feltéve, hogy a 2 metszéspont egyike nem esik

M M'

-re, mert így

A

D

C

egy egyenesben adódik. 1 megoldás esetén

A B C D

trapéznak adódik.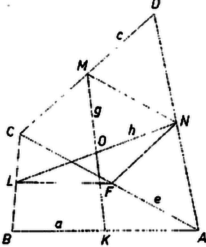

Boldizsár Ferenc (Kaposvár, Táncsics M. g. II. o. t.)

II. megoldás. Tovább is a fenti jelöléseket használva legyen az

A C

átló felezőpontja

F

. Így

L F

és

N F

A C B

, ill.

A C D

háromszög középvonala,

L F = a / 2

N F = c / 2

.
Megszerkesztjük az

e / 2

g / 2

h / 2

oldalakból az I. megoldás

M N O

háromszögét,

M

és

N

tükörképe

O

-ra

K

, ill.

L

. Az

L N = h

oldal fölé megszerkesztjük az

L N F

háromszöget. Az

F M N

háromszöget háromféleképpen kiegészítve paralelogrammává adódnak az

A

C

D

csúcsok,

B

pedig a

K F L B

paralelogramma negyedik csúcsa.
A szerkeszthetőség feltételei lényegében azonosak az I. megoldásban találtakkal. Az olvasóra bízzuk annak bizonyítását, hogy az

A B C D

négyszög megfelel a követelményeknek.

Lux Judit (Budapest, Móricz Zs. g. I. o. t.)