Feladat: 826. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Aczél G. ,  Berkes István ,  Bódi Zoltán ,  Bodonhelyi Márta ,  Bóta Károly ,  Fejes Tóth G. ,  Ferenczi György ,  Fiala István ,  Fodor L. ,  Gyenes Gábor ,  Göndör Gy. ,  Halász Szilvia ,  Herényi István ,  Hirka Ferenc ,  Hoffer Anna ,  Huhn András ,  Kéri Terézia ,  Kiss Árpád ,  Lovász László ,  Makai Endre ,  Mátrai Miklós ,  Pelikán József ,  Pintér J. ,  Pláveczky Gy. ,  Simig Gy. ,  Szabó Mihály ,  Székely Gábor ,  Szemkeő Judit ,  Szendrő P. ,  Szentai Judit ,  Szongoth Gábor ,  Takács Gy. ,  Török László ,  Varga Kornél 
Füzet: 1963/november, 146 - 147. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Tengelyes tükrözés, Mértani helyek, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1963/február: 826. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a C1C2C3C4C5=S szabályos ötszög középpontja O. Meghúzva a szimmetriatengelyeit, S feloszlik 10 derékszögű háromszögre. Közülük bármelyik kettő egymásba átvihető vagy egy O körüli forgatással, melynek szöge a 72∘-nak egy egész számú többszöröse, vagy valamelyik szimmetriatengelyen való tükrözéssel. Ezért elég egyelőre az OC1D háromszög belsejében vagy a kerületén levő P pontokra szorítkoznunk, ahol D a C4O tengely és a C1C2 oldal metszéspontja, egyben ezen oldal felezőpontja.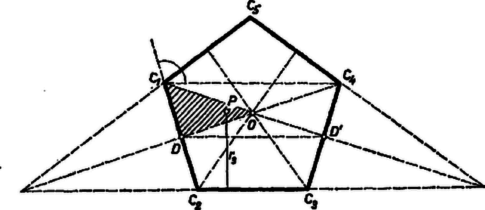

 
 

Megmutatjuk, hogy ekkor P-re nézve a C2C3 oldaltól mért távolság mindig megadja r3-at, vagyis van két másik a távolságok között, amelyik legfeljebb akkora, és kettő, amelyik legalább akkora, mint a C2C3 oldaltól mért távolság.
A P pont távolsága C2C3-tól legalább akkora, mint C1C2-től és C5C1-től, ugyanis a C1C2C3 szög C2O szögfelezőjének arra az oldalára esik, mint a C1C2 szár, vagy a szögfelezőre (ha P=O), másrészt a C2C3 és C1C5 oldalak közti szög C4D szögfelezőjének arra az oldalára, mint a C1C5 oldal, vagy a szögfelezőre.
Másrészt P távolsága C2C3-tól nem nagyobb, mint a C3C4 és C4C5 oldaltól mért távolsága, mert a C2C3C4 szög C3O szögfelezőjének a C2C3 szár felőli oldalára esik, vagy a felezőre; továbbá a C2C3 és C5C4 oldalak szögét felező C1O egyenesnek is arra az oldalára, mint a C2C3 szár, vagy a felezőre.
Azt kell még megvizsgálnunk, a C1DO háromszög melyik pontja van legmesszebb és melyik legközelebb a C2C3 oldalhoz. C1-en és D-n át párhuzamost húzva C2C3-mal, az előbbi átmegy C4-en, az utóbbi a C3C4 oldal D' felezőpontján. A két egyenes közti sáv tartalmazza az O pontot, s így a C1DO háromszöget, mert egyrészt
OC1C2∢=108∘2=54∘<C4C1C2∢=180∘-108∘=72∘,
másrészt
D'DC2=180∘-108∘=72∘<ODC2=90∘.
Eszerint a háromszög C1 csúcsa van legmesszebb és D csúcsa legközelebb C2C3-hoz, az utóbbi távolsága az előbbinek fele.
Most már P mindazon helyzetei, amelyekre r3 a lehető legnagyobb: S összes csúcsai, azok pedig, amelyekre r3 a lehető legkisebb: S összes oldalfelező pontjai.
 
 Szabó Mihály (Makó, József A. g. II. o. t.)
 
Megjegyzés. A távolságokat az oldalak egyeneseitől mértük. ‐ Egy pontnak egy szakasztól mért távolságán a szakasz hozzá legközelebbi pontjától mért távolságát értjük. Ha a pontnak a szakasz egyenesére való vetülete hozzátartozik a szakaszhoz, akkor a szakasztól való távolsága egyenlő az egyenestől való távolságával. Ha nem, akkor a szakasznak ahhoz a végpontjához van legközelebb a pont, amelyik közelebb van a vetületéhez. Könnyű belátni, hogy megállapításaink akkor is érvényesek, ha az ri(i=1, 2, ..., 5) távolságokat S oldalszakaszaitól mérjük.