|
| Feladat: |
825. matematika gyakorlat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bana I. , Bárány Imre , Berkes István , Bodonhelyi Márta , Boldizsár F. , Bulkai L. , Demetrovics J. , Fejes Tóth G. , Ferenczi György , Ferenczi S. , Gyenes Gábor , Harkányi Edit , Herényi István , Kersner R. , Kiss A. , Kiss Katalin , Kóbor Gy. , Körner János , Lovász László , Márki László , Mátrai Miklós , Molnár Ida , Móri A. , Nagy Klára , Nagy Zsuzsa , Pelikán József , Simon Gy. , Simonovits András , Somos I. , Szabó Mihály , Szabó Zoltán , Szamosvári Ágnes , Szeidl László , Székely Gábor , Szemkeő Judit , Szentai Judit , Szidarovszky Klára , Szutrély Judit , Tari P. , Treer Mária , Török László , Újvári Mária , Varga Kornél , Vesztergombi Katalin , Vitéz L. , Zomi L. |
| Füzet: |
1963/november,
145 - 146. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Derékszögű háromszögek geometriája, Numerikus és grafikus módszerek, Szögfüggvények, síkgeometriai számítások, Gyakorlat |
| Hivatkozás(ok): | Feladatok: 1963/február: 825. matematika gyakorlat |
|
|
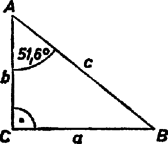
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen az derékszögű háromszögben m, , , , . A szögek radiánban vett mértékszámát is -val, -val jelöljük, ez nem okoz félreértést.
I. Az említett közelítő képletet mindkét hegyes szögre alkalmazva: elsőfokú egyenletrendszert kapunk -ra és -re: Innen | |
és értékét a közelítő értéket használva hibával kapjuk, tehát a negyedik értékes jegyben kis hibával. Másrészt és első értékes jegye százas helyi értékűnek várható, tehát 3 értékes jegyre kell számítanunk. Ezért az előkészítő számítások első lépéseiben 5, majd csak 4 értékes jegyet számítunk ki:
II. Másrészt a függvénytáblázat felhasználásával m, | |
Ezek szerint egyik számításunk hibája sem haladja meg a -ot.
Bárány Imre (Budapest‐Mátyásföld, Corvin Mátyás g. I. o. t.)
Megjegyzések. 1. Elegendő a közelítő képletet a kisebb szögre alkalmazni ‐ mert így kisebb a hiba ‐, ugyanis a másik egyenletet pótolhatjuk a Pythagorász‐tétellel. Így viszont másodfokú egyenletre jutunk, a számítás bonyolultabb:
és a két megoldás közül ki kell választanunk a megfelelőt. Innen és adódik, ezek a pontos értéktől valóban még kevésbé térnek el.
Ferenczi György (Budapest, I. István g. II. o. t.)
2. Sok dolgozatot nehezen ellenőrizhetővé tett a számadatok korai behelyettesítése. ‐ Néhányan ügyesen kihasználták, hogy jó közelítéssel és .
3. Lásd még az 1229. feladathoz fűzött 2. megjegyzést.
L. ezen számban, 133. o. |
|
 PDF
PDF