Kezdőlap


Feladat:	818. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gyenes Gábor
Füzet:	1963/december, 214 - 215. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai szerkesztések, Szabályos sokszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/január: 818. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az $A B C D E$ ötszög csúcsai az $S$ középpont körül $S D$ sugárral írt $k_{5}$ kerületén vannak, továbbá a 6. lépés szerint a $D C$ , $D E$ és $A B$ oldalak egyenlők. A $D S$ egyenes az ötszögnek szimmetriatengelye, mert mint a $P Q$ szakasz felező merőlegese, merőleges $A B$ -re, ‐ tehát fennáll az $A E = B C$ egyenlőség is: Elég tehát megmutatnunk, hogy $A S B ∢ = 72^{\circ}$ , mert így ugyanekkora a $C S D$ , $D S E$ szög is, tehát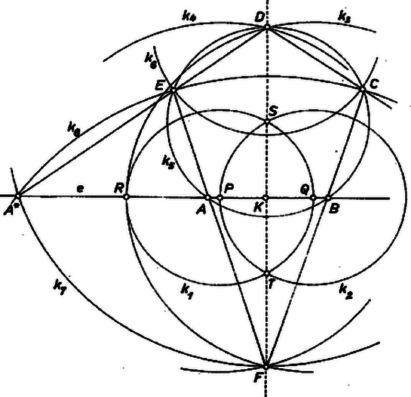

\begin{matrix} A S E ∢ = B S C ∢ = \frac{180^{\circ} - 3 \cdot 72^{\circ}}{2} = 72^{\circ}, \end{matrix}

ami az állítást igazolja.

Legyen

P Q

felezőpontja

K

. A

P Q S

és

P Q D

egyenlő szárú háromszögből,

Q R = 2 r

figyelembevételével

\begin{matrix} K S = \frac{r \sqrt[]{3}}{2}, K D = \frac{r \sqrt[]{15}}{2} = K S \sqrt[]{5}, \end{matrix}

ennélfogva

k_{5}

sugara

\begin{matrix} S A = S D = K D - K S = K S (\sqrt[]{5} - 1) . \end{matrix}

Így pedig az

A B S

egyenlő szárú háromszögből

\begin{matrix} cos A S K ∢ = \frac{K S}{A S} = \frac{1}{\sqrt[]{5} - 1} = \frac{\sqrt[]{5} + 1}{4}, \end{matrix}

ezért az 1157. feladat¹ szerint

A S K ∢ = 36^{\circ}

, tehát valóban

A S B ∢ = 72^{\circ}

II. Elég belátnunk, hogy az

E A

egyenes átmegy

F

-en, más szóval, hogy szabályos ötszögünk

108^{\circ}

-os

E A B

szöge a

B A F

szöggel együtt

180^{\circ}

-ot tesz ki. Szerkesztésnél fogva

B A F ∢ = B A D ∢ = A B D ∢

, ezért az

A B D

háromszög szögösszege és a kerületi szög tétele alapján

\begin{matrix} B A F ∢ = \frac{180^{\circ} - A D B ∢}{2} = 90^{\circ} - \frac{A S B ∢}{4} = 72^{\circ}, \end{matrix}

tehát az állítás helyes.

Gyenes Gábor (Budapest, I. István g. II. o. t.)

Megjegyzés.

C

-t és

E -

t a

k_{8} = F (F A^{*})

körrel is kimetszhetjük

k_{5}

-ből, ahol

A^{*}

k_{7} = S (S F)

körnek

e

-vel való egyik metszéspontja.

¹K. M. L. 25 (1962/11) 118. o.