Kezdőlap


Feladat:	816. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Iváncsy Szabolcs , Kelemen Gábor
Füzet:	1964/január, 17 - 20. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkidomok átdarabolása, Terület, felszín, Síkgeometriai számítások trigonometria nélkül négyszögekben, Síkgeometriai számítások trigonometria nélkül sokszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/január: 816. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az összes vonalakat meghúzva egy egységnyi oldalú $B_{1} B_{2} B_{3} B_{4}$ négyzetben, 5‐féle idom keletkezik: minden oldalon nyugszik 2‐2 egybevágó háromszög, ezekhez illeszkedik az oldalközéppontoknál 1‐1 kisebb, a négyzetcsúcsoknál 1‐1 nagyobb deltoid, a deltoidok további oldalaihoz 8 egybevágó kisebb háromszög csatlakozik, középen pedig egy egyenlő oldalú nyolcszög jön létre. Az ugyanolyan félének mondott idomok valóban egybevágók, mert a négyzetet középpontja körül $90^{\circ}$ valamilyen többszörösével elforgatva, ill. valamelyik átlóra vagy középvonalra tükrözve egymásba átvihetők. Jelöljük ezek területét a felsorolás sorrendjében $t_{1}$ , $t_{2}$ , $t_{3}$ , $t_{4}$ , ill. 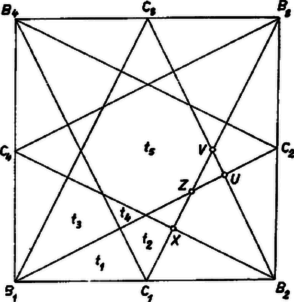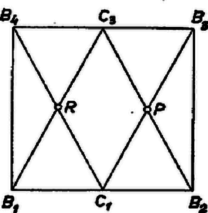$t_{5}$ -tel (1. ábra).

1. ábra

2. ábra

Jelöljük a

B_{1} B_{2}

B_{2} B_{3}

...

oldalak felezőpontját

C_{1}

C_{2}

C_{3}

C_{4}

-gyel és tekintsük először csak a

C_{1}

és

C_{3}

pontból induló vonalakat, a keletkező metszéspontok legyenek

P

és

R

(2. ábra). Így a négyzetet 1 rombuszra, 4 hegyesszögű és 2 tompaszögű háromszögre bontottuk: az utóbbiak mindegyike nyerhető a rombuszból valamelyik átlójával való szétvágással. Így a rombusz területe

1 / 4

, a háromszögeké

1 / 8

. Felírva, hogy az egyes idomok az 1. ábra milyen idomaiból tevődnek össze, a következő összefüggéseket kapjuk: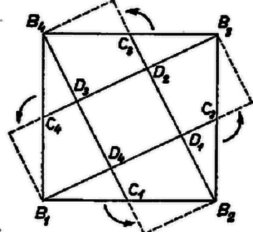

\begin{matrix} 2 t_{2} + 4 t_{4} + t_{5} = \frac{1}{4}, & (1) \\ t_{1} + t_{3} + t_{4} = \frac{1}{8}, & (2) \\ 2 t_{1} + t_{2} = \frac{1}{8} . & (3) \end{matrix}

3. ábra

Tekintsük most a

B_{1} C_{2}

B_{2} C_{3}

B_{3} C_{4}

B_{4} C_{1}

egyeneseket. Ezek egy

D_{1} D_{2} D_{3} D_{4}

négyzetet, 4 háromszöget és 4 trapézt határoznak meg (3. ábra). Ha a háromszögeket

C_{i}

csúcsuk körül (

i = 1

, 2, 3, 4)

180^{\circ}

-kal elforgatjuk, a trapézok a középsővel egybevágó négyzetekké egészülnek ki. Világos ugyanis, hogy a keletkező négyszögek téglalapok, de pl. a

B_{2} D_{1} D_{4} C_{1}

trapéz

B_{2}

csúcsához csatlakozó új oldal

B_{1} D_{4}

-gyel egyenlő hosszú, ez pedig

90^{\circ}

-os forgatással

B_{2} D_{1}

-be vihető át, tehát egyenlő vele. A kis négyzetek területe tehát

1 / 5

. A középsőt alkotó részidomokat felírva

\begin{matrix} 4 t_{4} + t_{5} = \frac{1}{5} . \end{matrix}

(4)

4. ábra

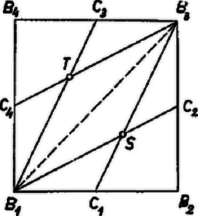Tekintsük végül a

B_{1}

és

B_{3}

csúcsból kiinduló osztóvonalakat, metszéspontjaik legyenek

S

és

T

(4. ábra). Ezzel a

B_{1} B_{2} B_{3}

és

B_{1} B_{3} B_{4}

háromszögek két‐két súlyvonalát húztuk meg. Így a

B_{1} S B_{3}

és

B_{1} T B_{3}

háromszögek

B_{1} B_{3}

oldalához tartozó magasságai harmadakkorák, mint a két derékszögű háromszög megfelelő magasságai, tehát a

B_{1} S B_{3} T

rombusz területe

1 / 3

. Felírva az alkotórészidomokat

\begin{matrix} 2 t_{3} + 4 t_{4} + t_{5} = \frac{1}{3} . \end{matrix}

(5)

Levonva (4)-et (1)-ből és (5)-ből, nyerjük, hogy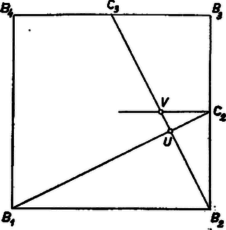

\begin{matrix} t_{2} = \frac{1}{2} (\frac{1}{4} - \frac{1}{5}) = \frac{1}{40}, t_{3} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5}) = \frac{1}{15} . \end{matrix}

Így (3)-ból, majd (2)-ből

\begin{matrix} t_{1} = \frac{1}{2} (\frac{1}{8} - \frac{1}{40}) = \frac{1}{20}, t_{4} = \frac{1}{8} - \frac{1}{20} - \frac{1}{15} = \frac{1}{120} . \end{matrix}

Végül (4)-ből

\begin{matrix} t_{5} = \frac{1}{5} - \frac{1}{30} = \frac{1}{6} . \end{matrix}

Iváncsy Szabolcs (Miskolc, Bláthy O. vill. t. I. o. t.)

5. ábra

II. megoldás. Húzzuk meg először a

B_{1} C_{2}

és

B_{2} C_{3}

szakaszokat, metszéspontjuk legyen

U

, és a

C_{2}

-ből

B_{1} B_{2}

-vel párhuzamosan húzott egyenes messe

B_{2} C_{3}

-at

V

-ben (5. ábra). Ekkor (az idomokat és területüket ugyanúgy ‐ csúcsaik egymás után írásával ‐ jelölve):

\begin{matrix} B_{2} B_{3} C_{3} = \frac{1}{4}, B_{2} C_{2} V = \frac{1}{4} \cdot B_{2} B_{3} C_{3} = \frac{1}{16}, \end{matrix}

továbbá, mivel a

C_{2} U V

és

B_{2} U C_{2}

háromszögek hasonlók, és átfogóik

C_{2} V = 1 / 4

B_{2} B_{3} C_{3}

háromszög középvonala), ill.

B_{2} C_{2} = 1 / 2

, így az előbbi háromszög területe az utóbbi negyedrésze, tehát a kettőből összetevődő

B_{2} C_{2} V

háromszög ötöde, így

\begin{matrix} C_{2} U V = \frac{1}{5} B_{2} C_{2} V = \frac{1}{5} \cdot \frac{1}{16} = \frac{1}{80}, és B_{2} U C_{2} = \frac{4}{5} \cdot \frac{1}{16} = \frac{1}{20} . \end{matrix}

Húzzuk most meg a

B_{2} C_{4}

és

B_{3} C_{1}

szakaszokat, messe az utóbbi a

B_{1} C_{2}

-t

Z

-ben (6. ábra). Ez a

B_{1} B_{2} B_{3}

háromszög súlypontja, s így a

B_{2} B_{3}

oldaltól

B_{1} B_{2} / 3 = 1 / 3

távolságra van, ennélfogva

\begin{matrix} B_{3} C_{2} Z = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{12} és \\ U V Z = B_{3} C_{2} Z - B_{3} C_{2} V - C_{2} U V = \frac{1}{12} - \frac{1}{16} - \frac{1}{80} = \frac{1}{120} . \end{matrix}

Jelöljük továbbá

B_{3} C_{1}

és

B_{2} C_{4}

metszéspontját

X

-szel, akkor

B_{2} X C_{1}

és

B_{2} U C_{2}

egymás tükörképei a

B_{2} B_{4}

átlóra nézve, így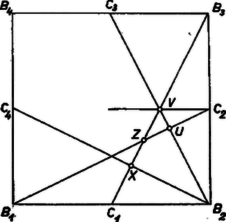

\begin{matrix} B_{2} U Z X = B_{2} B_{3} C_{1} - B_{3} C_{2} Z - B_{2} C_{2} U - B_{2} C_{1} X = \frac{1}{4} - \frac{1}{12} - 2 \cdot \frac{1}{20} = \frac{1}{15} . \end{matrix}

6. ábra

Meghúzva most már az összes osztóvonalakat (1. ábra), keletkezik 8 a

B_{2} U C_{2}

-vel egybevágó, tehát

t_{1} = 1 / 20

területű háromszög, 4 a

B_{2} U Z X

-szel egybevágó, tehát

t_{2} = 1 / 15

területű deltoid, 4 további, az oldalközéppontokhoz csatlakozó deltoid, amelyek

t_{3}

területe a

C_{2} U V

háromszög kétszerese, tehát

t_{3} = 2 C_{2} U V = 1 / 40

, 8 az

U V Z

-vel egybevágó háromszög, területük

t_{4} = 1 / 120

, végül egy nyolcszög, amelynek területe

\begin{matrix} t_{5} = 1 - 8 \cdot \frac{1}{20} - 4 \cdot \frac{1}{15} - 4 \cdot \frac{1}{40} - 8 \cdot \frac{1}{120} = \frac{1}{6} . \end{matrix}

Kelemen Gábor (Sárospatak, Rákóczi F. g. II. o. t.)