Kezdőlap


Feladat:	815. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Bodonhelyi Márta
Füzet:	1963/december, 211 - 213. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Középvonal, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/január: 815. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A következő szögek egyenlők:

\begin{matrix} C_{1} F_{2} F_{1} ∢, B C F_{1} ∢, A C F_{2} ∢, C_{1} F_{1} F_{2} ∢, \end{matrix}

mert az ábra szerint a felsorolás első két tagja egyállású szögpárt alkot, utolsó két tagja pedig váltószögpárt, végül a középső két szög az

A C B

szög felezésével keletkezett. Így

C_{1} F_{2} F_{1} ∢ = C_{1} F_{1} F_{2} ∢

, tehát

C_{1} F_{2} = C_{1} F_{1}

.
Hasonlóan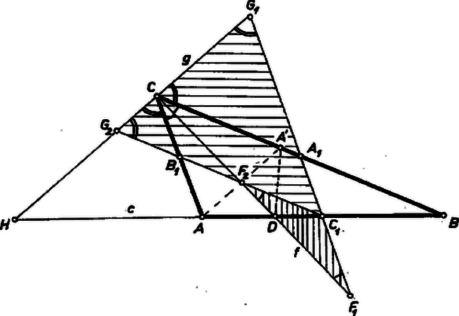

\begin{matrix} C_{1} G_{2} G_{1} ∢ = B C G_{1} ∢ = A C G_{2} ∢ = C_{1} G_{1} G_{2} ∢, \end{matrix}

mert a középső két szög az

A C B

szög felét derékszöggé egészíti ki, a szélső párok pedig egyállású szögek. Ezért

C_{1} G_{2} G_{1} ∢ = C_{1} G_{1} G_{2} ∢

, és

C_{1} G_{2} = C_{1} G_{1}

Szerkesztésnél fogva a

C_{1} F_{1}

egyenes átmegy a

B C

oldal

A_{1}

felezőpontján, mert az

A B C

háromszög

A C

-vel párhuzamos középvonala, ugyanis átmegy

C_{1}

-en és párhuzamos

A C

-vel,

C_{1} F_{2}

pedig ugyanígy az

A C

oldal

B_{1}

felezőpontján. Továbbá a fentiekből adódik, hogy a

B_{1} C F_{2}

és

A_{1} C G_{1}

háromszögek is egyenlő szárúak, így

\begin{matrix} C_{1} F_{2} & = C_{1} B_{1} - B_{1} F_{2} = A_{1} C - B_{1} C = \frac{B C - A C}{2}, \\ C_{1} G_{1} & = C_{1} A_{1} + A_{1} G_{1} = B_{1} C + A_{1} C = \frac{A C + B C}{2}, \end{matrix}

vagyis a vizsgálandó szárak hossza egyenlő az eredeti háromszög

C

-ben összefutó oldalainak fél különbségével, ill. fél összegével.

Bodonhelyi Márta (Budapest, Móra F. lg. II. o. t.)

Megjegyzések. 1. A felhasznált szögpárok egyenlősége és

C_{1} F_{2}

hosszának meghatározása épít a következő, szemléletre és a

B C > A C

feltevésre alapozott tényekre:

α

)

f

A B

egyenes

A C_{1}

szakaszát metszi,

β

) az

f

egyenesen

C

F_{2}

F_{1}

sorrendben következnek a kijelölt pontok,

γ

)

G_{1}

és

G_{2}

pedig közrefogja

C

-t

g

-n. Ezeket beláthatjuk a szemléletre való hivatkozás nélkül is.

α

)

f

-nek az

A B

egyenessel való

D

metszéspontja az oldalszakaszra esik, mert

f

belső szögfelező. Jelöljük

A

-nak

f

-re vett tükörképét

A'

-vel, ez a feltevés szerint a

B C

szakaszon van. Így az

A' B D

háromszögben

\begin{matrix} B A' D ∢ & = 180^{\circ} - C A' D ∢ = 180^{\circ} - C A B ∢ = \\ = A B C ∢ + A C B ∢ > A B C ∢ = D B A' ∢, \end{matrix}

tehát a szemben fekvő oldalakra

B D > A' D = A D

β

) A

B_{1} C_{1}

egyenes

B_{1}

-ben metszi az

A C D

háromszög kerületét, tehát még egy pontban kell metszenie. Ez nem lehet az

A D

oldalon, mert annak meghosszabbítását metszi

B_{1} C_{1}

(C_{1}

-ben), tehát

B_{1} C_{1}

-nek

f

-fel való

F_{2}

metszéspontja a

C D

szakaszon van.
Az

A C D

háromszög az

A_{1} C_{1}

egyenesnek teljesen egyik partján fekszik, mert

C_{1}

A D

szakasz

D

-n túli meghosszabbításán van,

A C

pedig párhuzamos

A_{1} C_{1}

-gyel. Így a

C D

egyenest

A_{1} C_{1}

C D

szakaszon kívül metszi, mégpedig

D

-n túli meghosszabbításában, mert az

A C

egyenesnek a

D

pont s vele együtt

f

-nek a

C

-ből

D

felé haladó félegyenese esik ugyanazon oldalára, mint

A_{1} C_{1}

. Így a

C

F_{2}

D

F_{1}

pontok ebben a sorrendben következnek az

f

egyenesen.

γ

) A

g

egyenes az

A C B

szögtartományon kívül halad, mert e szög

180^{\circ}

-nál kisebb, így

G_{1}

C_{1} A_{1}

szakasz

A_{1}

-en túli meghosszabbítására,

G_{2}

pedig

C_{1} B_{1}

-nek

B_{1}

-en túli meghosszabbítására esik.

F_{2}

A C

és

A_{1} C_{1}

egyenesek közt van, mert

C

és

F_{1}

közt van, így egyszersmind

B_{1}

és

C_{1}

közt, tehát a

C_{1} G_{2}

szakaszon van.

F_{1}

viszont

C D

-nek

D

-n túli meghosszabbításán van, így

A B

-nek ellenkező oldalán, mint

C

és mint

A_{1}

. Így

F_{1}

A_{1} C_{1}

szakasz

C_{1}

-en túli meghosszabbításán van. Eszerint az

f

egyenes a

C_{1} G_{1} G_{2}

háromszög

C_{1} G_{2}

oldalát és a

G_{1} C_{1}

oldal meghosszabbítását metszi, kell tehát, hogy a harmadik oldalt messe, azzal való

C

metszéspontja

G_{1}

és

G_{2}

közt legyen.
2. A

C_{1} G_{1} = C_{1} G_{2}

egyenlőséget így is bizonyíthatjuk. A

G_{1} C_{1} G_{2}

szög

f_{1}

felezője párhuzamos

f

-fel, mert a szög váltószög‐párja

A C B ∢

-nek, és váltószögek felezői párhuzamosak. Így

f_{1}

merőleges

g

-re. Ha pedig egy háromszög egy szögfelezője merőleges a szemben levő oldalra, akkor a háromszög egyenlő szárú. Itt viszont a dőlt betűvel szedett állításokat kellene bizonyítanunk.
3. A vizsgált háromszögek szárainak az

A B

B C

C A

oldalakkal való kifejezéseit néhány dolgozat a belső és külső szögfelezők

A D : D B = A C : C B = A H : H B

osztásarányát felhasználva több számítással állította elő.