Feladat: 801. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Pelikán József 
Füzet: 1963/november, 140 - 142. oldal  PDF  |  MathML 
Témakör(ök): Középvonal, Párhuzamos szelők tételének megfordítása, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1962/november: 801. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Képzeljük a feladatot megoldottnak. Megmutatjuk, hogy az F-en át BC-vel párhuzamosan húzott egyenes felezi a DE szakaszt. Jelöljük ki az AC oldal G felezőpontját és DE-n az F1 felezőpontot. Ekkor F a CG felezőpontja, továbbá DG az ABC háromszög középvonala, így párhuzamos BC-vel. Ennek folytán a CEDG négyszög trapéz és FF1 a középvonala, tehát párhuzamos 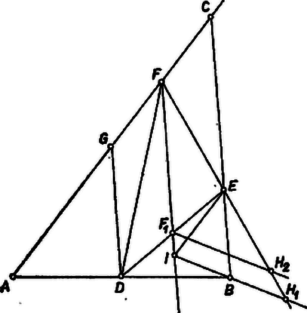BC-vel.

 
 
1. ábra
 

Mivel az F ponton át BC-vel párhuzamosan húzott egyenes egyértelműen meg van határozva, így ha fordítva járunk el: F-en át húzunk párhuzamost BC-vel, akkor is annak a DE szakasz F1 felezőpontján kell átmennie.
A középvonalak hosszára vonatkozó összefüggések alapján FF1 hosszából meg tudjuk határozni CE hosszát.
DG=12BC=12⋅32⋅CE=34CEésFF1=12(DG+CE)=78CE,azazCE=87FF1.



Ennek alapján meg tudjuk határozni C-t, abból B-t, majd CF és BD metszéspontjaként A-t. Pl. a következőképpen járhatunk el (előrebocsátjuk, hogy D, E, F egy háromszög oldalainak belső pontjai, így nem lehetnek egy egyenesen).
Szerkesszük meg DE-n az F1 felezőpontot, FE-nek E-n túli meghosszabbítására pedig mérjük rá az EH1=EF és EH2=34EF távolságot. Legyen a H1-en át H2F1-gyel párhuzamosan húzott egyenes és az FF1 egyenes metszéspontja I. Ekkor FI=87FF1. Szerkesszük meg az ezzel egyenlő és párhuzamos EC szakaszt a DE egyenesnek azon az oldalán, amelyiken F van. Legyen a szakasz meghosszabbításának metszéspontja H1I-vel B. Ekkor EB az FH1I háromszög középvonala, így az FI=CE szakasz felével egyenlő. E tehát a BC szakasz B felőli harmadoló pontja. A-t úgy kapjuk, mint BD és CF metszéspontját.
Messe a D-n át BC-vel párhuzamosan húzott egyenes AC-t G-ben. A CEDG trapéz FF1 középvonalára (DG+CE)/2=FF1 innen
DG=2FF1-CE=(2⋅78-1)CE=34CE=34⋅23BC=12BC,
DG tehát az ABC háromszög középvonala, D és G az AB és AC oldalak felezőpontja, F pedig a CA oldal C-hez közelebbi negyedelő pontja. Ezzel a szerkesztés helyességét bebizonyítottuk.
A szerkesztés minden lépése egyértelmű. A háromszög létrejön, a BD és CF egyenesek ugyanis nem párhuzamosak, mert CF∥EI és I a DE egyenesnek ugyanarra az oldalára esik, mint B, a BE egyenesnek pedig ugyanarra az oldalára, mint D. Ebből következik, hogy az EI egyenes a BED szögtartományban halad, tehát metszi a B-ből D-n át húzott félegyenest.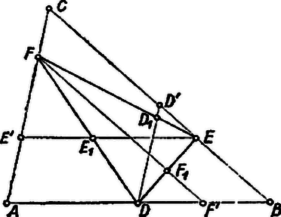
 
 
2. ábra
 

Megjegyzés. Meghatározhatnánk F1-éhez hasonlóan annak a D1, ill. E1 pontnak az osztásarányát a DEF háromszög kerületén, amelyet a D-n át AC-vel, ill. E-n át AB-vel párhuzamosan húzott egyenes metsz ki a szemközti EF, ill. FD oldalból (ED1:EF=1:4, FE1:FD=5:9). Ennek alapján megszerkeszthetnénk a három oldal irányát és ebből a keresett háromszöget. Az így adódó szerkesztés helyességének igazolása azonban lényegesen bonyolultabb lenne, mint a föntié. Számos versenyző az utóbbi eljárást adta meg ‐ igazolás nélkül.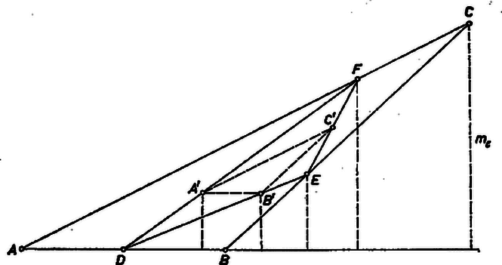
 
 
3. ábra
 

II. megoldás (részlet). Osszuk ketté az ED szakaszt a B' ponttal a CA oldalra előírt arányban, vagyis legyen EB':ED=CF:CA=1/4=z, továbbá a DF oldalt az A' ponttal a BC oldalra előírt arányban: DA':DF=BE:BC=1/3=y. Ekkor A'B' párhuzamos AB-vel. Ugyanis A'-nek AB-től való távolsága y-szor akkora, mint F távolsága AB-től, ez pedig (1-z)-szerese az ABC háromszög mc magasságának, tehát A' távolsága y(1-z)mc, másrészt hasonlóan ugyanezt a kifejezést kapjuk B'-nek AB-től való távolságára. Ha még az FE oldalon úgy szerkesztjük C'-t, hogy álljon FC':FE=AD:AB=1/2, akkor hasonlóan A'C'∥AC és B'C'∥BC, tehát az ABC háromszög oldalegyeneseit úgy kapjuk, hogy vesszük D-n, E-n, F-en át rendre az A'B'-vel, ill. B'C'-vel, ill. C'A'-vel párhuzamos egyenest.
 
 Pelikán József (Budapest, Fazekas M. gyak. g. I. o. t.)