Feladat:	787. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Aczél Gábor ,  Szentai Judit
Füzet:	1963/október, 66 - 70. oldal		PDF  |  MathML
Témakör(ök):	Szögfelező egyenes, Húrnégyszögek, Érintőnégyszögek, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1962/október: 787. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.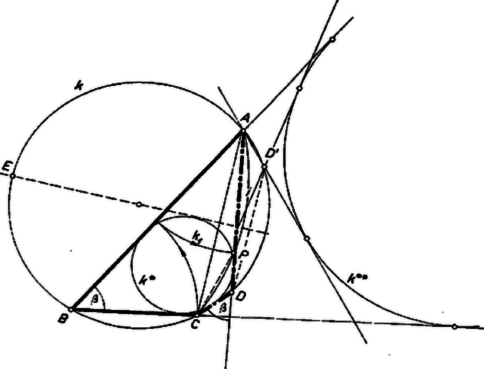     1. ábra   I. megoldás. Olyan $D$ pontot keresünk, amellyel az $ABCD$ négyszög oldalait érintő kör a négyszög belsejében van. Ekkor, mint ismeretes, $AB+CD=BC+AD$. Gondoljuk megoldottnak a feladatot és válasszuk a betűzést úgy, hogy álljon $AB\ge BC$. ($AB=BC$ esetén nyilvánvaló, hogy $D$ a $B$-vel átellenes pont. Az $AB<BC$ esetben $DA>DC$.) Mérjük rá $DA$-ra a $DP-DC$ szakaszt (1. ábra). Így egyrészt $\begin{array}{c}{\displaystyle AP=AD-DP=AD-CD=AB-BC\mathrm{,}}\end{array}$ (1) ismert. Másrészt a $CDP$ háromszög egyenlő szárú, $D$-nél levő külső szöge egyenlő az $ABC=\beta$ szöggel, mert $ABCD$ húrnégyszög, ezért $CPD\sphericalangle =\beta /2$ és $APC\sphericalangle ={180}^{\circ }-\beta /2$. Ezek szerint az $APC$ háromszögben ismerjük az $AP$, $AC$ oldalakat és az utóbbival szemben fekvő szöget. Ezek alapján megszerkeszthetjük $P$ helyzetét. $P$ egyrészt az $A$ körül $AP$ sugárral írt $k_1$ körön van, másrészt azon az $i$ köríven, amelyről $AC$ látószöge ${180}^{\circ }-\beta /2$, és amely az $AC$ egyenes $D$-vel egyező, tehát $B$-vel ellentétes oldalán van. $i$ középpontjából $AC$-t $2CPD\sphericalangle =\beta$ szögben látjuk ‐ ugyanúgy, mint $B$-ből ‐, ezért az $i$-t tartalmazó kör $E$ középpontját $k$-ból $AC$ felező merőlegese metszi ki. $P$ ismeretében a keresett $D$-t az $AP$ egyenes metszi ki 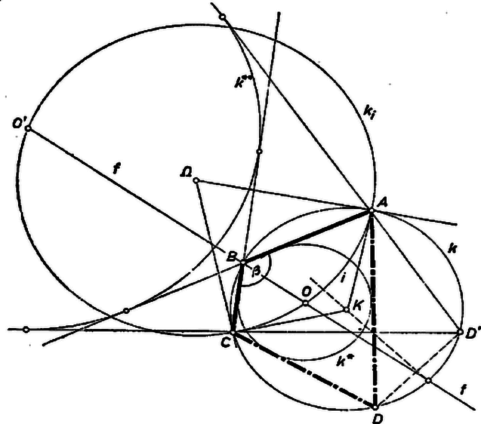$k$-ból.     2. ábra   $P$ mindig létrejön, mert $k_1$ középpontja az $i$ végpontjában van, és $k_1$ sugara kisebb az $i$-hez tartozó $AC$ húrnál, ugyanis az $ABC$ háromszögből $AP=AB-BC<AC$. Éspedig $P$ a $k$ belsejében van, mert $i$-re is ez áll; ugyanis $i$ pontjaiból $AC$-t nagyobb szögben látjuk, mint a $k$-hoz tartozó, $D$-t tartalmazó $AC$ ív pontjaiból, hiszen ${180}^{\circ }-\beta /2>{180}^{\circ }-\beta$. $P$-re mindig 1 megoldást kapunk. A kapott $D$ pont megfelel a követelménynek. Ugyanis $k$-nak $B$-t nem tartalmazó $AC$ ívén van, ezért $ADC\sphericalangle ={180}^{\circ }-\beta$, így a $CDP$ háromszögből $\begin{array}{c}{\displaystyle PCD\sphericalangle =APC\sphericalangle -ADC\sphericalangle =\left({180}^{\circ }-\frac{\beta }{2}\right)-\left({180}^{\circ }-\beta \right)=CDP\sphericalangle \mathrm{,}}\end{array}$ tehát ez a háromszög egyenlő szárú, $CD=DP$, így $\begin{array}{c}{\displaystyle DA-DC=AB-BC\mathrm{,}\text{vagyis}DA+BC=AB+DC\mathrm{.}}\end{array}$ Ez pedig elegendő feltétele annak, hogy az $ABCD$ (konvex) négyszög belsejébe lehessen beírni az oldalakat érintő kört. ‐ Ezzel a feladat megoldását befejeztük.    Aczél Gábor (Budapest, Apáczai Csere J. gyak. g. II. o. t.) dolgozata,  bizonyítással és diszkusszióval kiegészítve.   II. megoldás. Megszerkesztjük a beírt $k^{*}$ kör $O$ középpontját (2. ábra). Ezt ismerve megrajzolhatjuk $k^{*}$-ot, mert az $ABCD$ négyszög $AB$, $BC$ oldalai ismertek, így pedig $D$-t az $A$-ból $k^{*}$-hoz húzott második érintővel metszhetjük ki $k$-ból. $O$ egyrészt rajta van az ismert $ABC$ szög felezőjén, úgyszintén $DAB$ és $DCB$ szögek felezőjén is. Másrészt az $ABCO$ négyszögben $\begin{array}{c}{\displaystyle AOC\sphericalangle ={360}^{\circ }-ABC\sphericalangle -\left(OAB\sphericalangle +OCB\sphericalangle \right)\mathrm{.}}\end{array}$ A zárójelben a $DAB$ és $DCB$ szögek összegének fele áll, ez pedig ${90}^{\circ }$, mert $ABCD$ húrnégyszög, tehát a mondott szögek összege ${180}^{\circ }$. Így $\begin{array}{c}{\displaystyle AOC\sphericalangle ={270}^{\circ }-\beta \mathrm{,}}\end{array}$ ismert. Ezzel második mértani helyet kaptunk $O$-ra. Ha ugyanis $\beta$ hegyesszög, akkor a számított szög nagyobb ${180}^{\circ }$-nál, az $ABCO$ négyszög konkáv, $O$ az $ABC$ háromszögben van, így a kisebb $AOC$ szög, $AC$-nek $O$-ból vett látószöge ${360}^{\circ }-\left({270}^{\circ }-\beta \right)={90}^{\circ }+\beta$, ismert, tehát $O$ az $AC$-nek ${90}^{\circ }+\beta$ nyílású látószögkörívén van, $AC$-nek $B$-vel egyező oldalán. (A $\beta <{90}^{\circ }$ tény fennállását láthatjuk abból, hogy $k$-nak $K$ középpontja az $ABC$ háromszögben van; $k$-val együtt természetesen $K$-t is adottnak tekinthetjük.) Ha $\beta$ tompaszög ($K$ kívül van az $ABC$ háromszögön, a 2. ábrán ez az eset látható), akkor a fent számított szög tompaszög, ez adja $AC$-nek $O$-ból vett látószögét. Ha végül $\beta$ derékszög ($K$ rajta van az $AC$ szakaszon), akkor $O$-t az $ABC$ szög felezője kimetszi $AC$-ből, $k^{*}$ tükrös $AC$-re, és így $D$ a $B$-nek $AC$-re vett tükörképe. Ekkor $ABCD$ deltoid. Ezt az esetet tovább mellőzhetjük. Keressük meg az $i$-t tartalmazó $k_i$ kör $\Omega$ középpontját. Ez mindkét esetben $AC$-nek $O$-val ellentétes partján van, mert a ${90}^{\circ }+\beta$, ill. ${270}^{\circ }-\beta$ látószög tompaszög. Láttuk, hogy $O$ az $AC$-nek mindig ugyanazon oldalán van, mint $K$, ezért $AC$ mindig elválasztja $\Omega$-t $K$-tól. $k_i$-nek az $AOC$ szög szárai közti ívéhez $\Omega$-ban ${180}^{\circ }$-nál nagyobb középponti szög tartozik, ezért a kisebb $A\Omega C$ szög ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \beta <{90}^{\circ }}& {\displaystyle \text{esetén}{360}^{\circ }-2\left({90}^{\circ }+\beta \right)={180}^{\circ }-2\beta \mathrm{,}}\hfill \\ \hfill {\displaystyle \beta >{90}^{\circ }}& {\displaystyle \text{esetén}{360}^{\circ }-2\left({270}^{\circ }-\beta \right)=2\beta -{180}^{\circ }\mathrm{.}}\hfill \end{array}}$ Ezért az első esetben $\Omega AC\sphericalangle =\Omega CA\sphericalangle =\beta$, tehát $A\Omega$ a $k$-hoz $A$-ban, $C\Omega$ pedig a $C$-ben húzott érintő. ‐ Ugyanerre jutunk a második esetben is, mert $\begin{array}{c}{\displaystyle \Omega AC\sphericalangle =\Omega CA\sphericalangle ={180}^{\circ }-\beta }\end{array}$ (hegyesszög, ekkor $\Omega$ azon az oldalán van $AC$-nek, mint $B$). Mindezek alapján $O$-t a következő lépésekben kapjuk: meghúzzuk $k$ érintőjét $A$-ban és $C$-ben, metszéspontjuk $\Omega$; $\Omega$ körül $\Omega A=\Omega C$ sugárral megrajzoljuk a rövidebb $AC=i$ ívet; megszerkesztjük az $ABC$ szög $f$ felezőjét; $i$ és $f$ metszéspontja $O$. A szerkesztés helyességének bizonyítását és diszkusszióját hely hiányában ‐ az olvasóra bízzuk.    Szentai Judit (Budapest, Kanizsay D. lg. II. o. t.) dolgozata,  kiegészítve $i$ megszerkesztésével.   Megyjegyzések. 1. Az érintőnégyszög oldalegyeneseit érintő kör eshet a négyszögön kívül is. Könnyen igazolható, hogy ilyenkor a négyszög valamelyik két szomszédos oldalának összege egyenlő a másik két oldal összegével. A 2. ábrán a négyszög negyedik csúcsa $D\text{'}$ és $AB+AD\text{'}=CB+CD\text{'}$. Ezt $AB-BC=CD\text{'}-AD\text{'}$ alakban írva és (1)-nek $AB-BC=AD-CD$ alakjával összehasonlítva csak annyi a változás, hogy a jobb oldalon $C$ és $A$ felcserélődött. Eszerint $D\text{'}$-t $D$-nek $AC$ felező merőlegesére való tükrözésével kapjuk ($\beta ={90}^{\circ }$ esetén ilyen megoldás nincs). 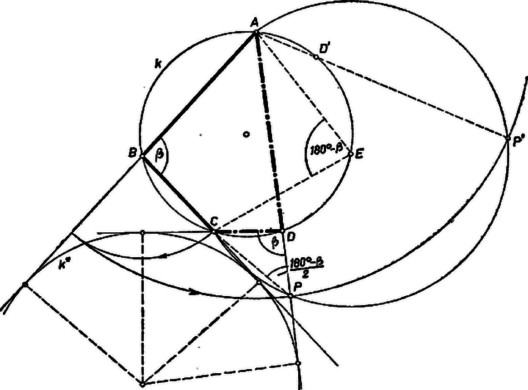    3. ábra   Ajánljuk az olvasóknak, járják végig mindkét megoldás gondolatmenetét erre az esetre is (l. az ábrákat). Hasonlóan tárgyalható a 3. ábra esete is, amikor 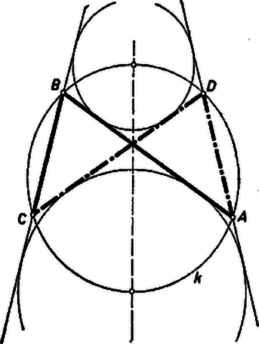$AB+BC=AD+DC$.     4. ábra   2. Könnyen belátható, hogy ha $D$-t az $AB$-nek $C$-t nem tartalmazó partján úgy vesszük, hogy $AD=BC$ (4. ábra), akkor a hurkolt $ABCD$ szimmetrikus húrnégyszöghöz két olyan kör is van, mely mind a négy oldalegyenest érinti. (Ugyancsak két érintő kör van a fenti $\beta ={90}^{\circ }$, deltoid esetében is.) 3. A dolgozatok alig tartalmaznak bizonyítást és diszkussziót. Ezt a tanév adott időszakában az I. osztályosok részéről természetesnek vettük, a II. és III. osztályosok részéről viszont hiánynak minősítettük. (Az 1. és 2. megjegyzésben említett lehetőségek mellőzését nem tekintjük hiánynak.)