Kezdőlap


Feladat:	783. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Dankó István
Füzet:	1963/március, 146 - 147. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1962/szeptember: 783. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a körök a fenti felsorolás rendjében $k_{1}$ , $k_{2}$ , $k_{3}$ , $k_{4},$ középpontjaik rendre $O_{1} \equiv O_{2} \equiv O$ , $O_{3}$ , $O_{4}$ , sugaraik rendre $r_{1}$ , $r_{2}$ , $r_{3}$ , $r_{4}$ . Feltehetjük, hogy $r_{1} > r_{2}$ . Így $k_{3}$ és $k_{4}$ csak a $k_{1}$ és $k_{2}$ közti körgyűrűben haladhatnak, $k_{1}$ -et mindkettő belülről érinti. $O_{3}$ és $O_{4}$ egymástól és $O$ -tól különböző pontok. Az $O O_{3} = t$ egyenesen rajta van a $k_{1}$ , $k_{3}$ körpár $E_{13}$ érintkezési pontja, úgyszintén a $k_{2}$ , $k_{3}$ pár $E_{23}$ érintkezési pontja is. E két pont egymástól különböző, mert $k_{1}$ -nek és $k_{2}$ -nek nincs közös pontja. Ezért az érintkezési pontok közös egyenese csak az $O O_{3}$ -mal azonos $E_{13} E_{23}$ egyenes lehet. Ezen van tehát a $k_{3}$ , $k_{4}$ körpár $E_{34}$ érintkezési pontja is, ennélfogva $O_{4}$ is, tehát $t$ az egész ábra szimmetriatengelye.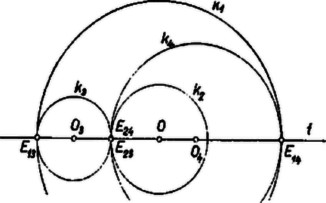

1. ábra

k_{3}

-nak

t

-n levő pontjai

E_{13}

és

E_{23}

, a

k_{4}

-gyel való érintkezése csak

E_{23}

-ban lehetséges, mert

E_{34} \equiv E_{13}

esetén

k_{3}

és

k_{4}

belülről érintkeznének. Így

E_{23}

egyszersmind a

k_{2}

k_{4}

körpárnak is érintkezési pontja. Mivel

O_{3}

és

O_{4}

E_{23} \equiv E_{34}

-nek két oldalán van, azért

k_{3}

és

k_{4}

egyike kívülről érinti

k_{2}

-t, másikuk pedig magában foglalja azt. (Nem lehet, hogy

k_{2}

foglalja magában e körök egyikét, mert

k_{3}

-nak is,

k_{4}

-nek is van

k_{2}

-n kívüli pontja: a

k_{1}

-gyel való érintkezési pontjuk.) Válasszuk az indexezést úgy, hogy

k_{4}

foglalja magában

k_{2}

-t. Végül

k_{1}

és

k_{4}

egymást a

t

-n levő,

E_{13}

-tól különböző

E_{14}

pontjukban érintik (1. ábra).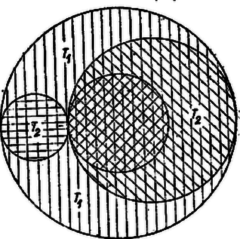

2. ábra

Ezek szerint a

k_{2}

k_{3}

k_{4}

körök

k_{1}

belsejét 5 részre osztják (2. ábra). Nincs olyan terület, melyet mind a 4 kör fedne, mert

k_{3}

-nak és

k_{4}

-nek nincs közös belső pontja.

k_{2}

területét még

k_{1}

is,

k_{4}

is lefedi, ez 3-szor fedett terület, a bizonyításban figyelmen kívül marad. Kétszer fedett a

k_{3}

egész területe, valamint

k_{4}

-nek

k_{2}

-n kívüli része, mert

k_{1}

-be is beletartoznak; így a 2-szer fedett területek összege

\begin{matrix} T_{2} = r_{3}^{2} π + (r_{4}^{2} π - r_{2}^{2} π) . \end{matrix}

Egyszer van fedve

k_{1}

-nek a

k_{3}

-on és

k_{4}

-en kívüli része, ennek területe

\begin{matrix} T_{1} = r_{1}^{2} π - r_{3}^{2} π - r_{4}^{2} π . \end{matrix}

Képezzük

T_{1}

és

T_{2}

különbségét. Ha ezt 0-nak találjuk, az állítást bebizonyítottuk.

\begin{matrix} T_{1} - T_{2} = π [r_{1}^{2} + r_{2}^{2} - 2 (r_{3}^{2} + r_{4}^{2})], \end{matrix}

és mivel

\begin{matrix} r_{3} = \frac{r_{1} - r_{2}}{2}, r_{4} = \frac{r_{1} + r_{2}}{2}, \end{matrix}

azért valóban

\begin{matrix} T_{1} - T_{2} = π (r_{1}^{2} + r_{2}^{2} - \frac{2 r_{1}^{2} + 2 r_{2}^{2}}{2}) = 0. \end{matrix}

Dankó István (Tokaj, Tokaji F. g. II. o. t.)