Kezdőlap


Feladat:	774. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Keresszegi Hajnalka , Mátrai Miklós
Füzet:	1963/február, 70 - 72. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Négyszögek szerkesztése, Gyakorlat, Középpontos és egyéb hasonlósági transzformációk
Hivatkozás(ok):	Feladatok: 1962/május: 774. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Képzeljük megoldottnak a feladatot, és legyen a keresett trapéz $A B C D$ , melyben $A B ∥ C D$ , $A B = a$ és $C D = c$ az adott szakaszok, $C A D ∢ = α$ és $A C B ∢ = γ$ az adott szögek. Feltehetjük, hogy $a \geq c$ , ekkor a $C$ -n át $A D$ -vel húzott párhuzamos $A B$ -t vagy egy belső $E$ pontban metszi, vagy $B$ -ben, ezér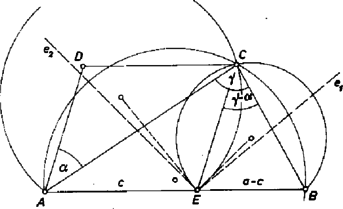t $γ = A C B ∢ \geq A C E ∢ = C A D ∢ = α$ .

1. ábra

Innen azt is látjuk, hogy ismerjük

A B

-nek és

A E = c

E B = a - c

részeinek

C

-ben vett látószögét, ugyanis

B C E ∢ = γ - α

. Ezért

A

B

és

E

kijelölése után (ti.

A E = c

) a 3 látószögkörív közül bármelyik kettőt megrajzolva metszéspontjukban megkapjuk

C

-t, majd az

A E C

háromszöget

A E C D

paralelogrammává kiegészítve

D

-t. (A szimmetria miatt a látószögköríveket elég

A B

-nek egyik partján megrajzolni.)

E B

látóköríve csak

a - c > 0

, valamint

γ - α > 0^{\circ}

, azaz

a > c

és

γ > α

mellett használható. E feltételek teljesülése esetén mindig van megoldás. Vegyük ugyanis

A E

-nek

α

nyílású és

E B

-nek

γ - α

nyílású látószögkörívét, és rajzoljuk meg

E

-beli érintőjüknek a használt félsíkon levő

e_{1}

ill.

e_{2}

félegyenesét. Az első félérintő az

E A

félegyenessel

180^{\circ} - α

szöget, a második félérintő

E B

-vel

180^{\circ} - (γ - α)

szöget zár be, ekkora szögben látjuk az egyes íveket

E

-ből. E két szög összege

360^{\circ} - γ

, és ez nyilván nagyobb

180^{\circ}

-nál, mert

γ < 180^{\circ}

. A

180^{\circ}

-kal szemben mutatkozó

180^{\circ} - γ

többlet megadja a két félérintő közti szög (a szögtartományokkal kétszer lefedett szög) nagyságát. Ebben a szögben mindkét ívet látjuk, tehát van egyetlen közös pontjuk, és az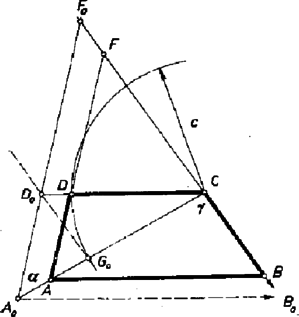

C

Keresszegi Hajnalka (Pápa, Petőfi S. g. II. o. t.)

II. megoldás. Feltesszük, hogy

c < a

és

γ > α

. Ekkor a szárak

C

-n, ill.

D

-n túli meghosszabbításai metszik egymást egy

F

pontban. A külső szög tétele szerint

A F C ∢ = A C B ∢ - C A F ∢ = γ - α

, ennélfogva szerkeszthetünk egy az

A C F

-hez hasonló

A_{0} C_{0} F_{0}

háromszöget. Ezt kiegészítjük egész alakzatunk nagyított (vagy kicsinyített) képévé.

F D C

és

F A B

hasonló háromszögek, ezért

F D : F A = c : a

, ennek alapján az

F_{0} A_{0}

oldalon megszerkeszthetjük a

D

-nek megfelelő

D_{0}

pontot. Most már

B_{0}

-t

F_{0} C_{0}

-ból a

D_{0} C_{0}

-lal

A_{0}

-on át húzott párhuzamos metszi ki, végül az

A_{0}

B_{0}

C_{0}

D_{0}

F_{0}

pontok alakzatát úgy nagyítjuk, hogy pl.

C_{0} D_{0}

megfelelője egyenlő legyen

c

-vel.

2. ábra

Egy célszerű végrehajtás: Egy

a

hosszúságú

A_{0} C_{0}

szakasz egyik partjára

A_{0}

-ban felmérjük

α

-t, a másik partjára

C_{0}

-ban

γ

-t; ekkor

α

és

γ

szabad szárainak metszéspontja

F_{0}

. Mérjük fel

C_{0}

-tól

A_{0}

felé

c

-t, jelöljük a végpontot

G_{0}

-lal, ekkor

D_{0}

-t a

G_{0}

-on át

C_{0} F_{0}

-lal párhuzamosan húzott egyenes metszi ki

A_{0} F_{0}

-ból.

B_{0}

megszerkesztése mellőzhető. Vegyük most

C

-t azonosnak

C_{0}

-lal, tehát ez lesz a nagyítás középpontja. Ekkor

D

-t a

C_{0} D_{0}

félegyenesen kapjuk

C

-től

c

távolságban (a felmérés elmaradhat, ha

G_{0}

kitűzésekor

C

körül

c

sugarú kört írtunk),

A

-t a

D

-n átmenő

A_{0} F_{0}

-lal párhuzamos metszi ki

C_{0} A_{0}

-ból,

B

-t pedig az

A

-n át

C_{0} D_{0}

-lal párhuzamosan húzott egyenes

C F_{0}

-ból.
A mondott szerkesztések egyértelműen végrehajthatók, tehát a feladatnak 1 megoldása van.

Mátrai Miklós (Hódmezővásárhely, Bethlen G. g. I. o. t.)