Kezdőlap


Feladat:	767. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Antal Magdola , Bak Zsuzsanna , Deák István , Ferenczi Gy. , Fiala István , Földes Antónia , Gazsó J. , Gecsey László , Gerencsér L. , Gerencsér László , Harkányi G. , Harkányi Gábor , Hirka András , Kohut József , Lehel Csaba , Lőrincz Cs. , Major Pál , Mátrai M. , Mészáros György , Nagy Klára , Radó Iván , Ruda M. , Simon István , Stiga Katalin , Strommer R. , Széchy Gy. , Szentai Judit , Szidarovszky Klára , Tamás Endre , Tihanyi László
Füzet:	1963/március, 135 - 137. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Tengelyes tükrözés, Oldalfelező merőleges, Körülírt kör, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1962/április: 767. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tükrözzük a $J K L$ háromszöget a $J K$ oldal felező merőlegesére, legyen $L$ tükörképe $M$ (1. ábra). A $J M$ szakasz húrja a $J K L$ háromszög $k$ körülírt körének, mert a tükrözés tengelye ennek a körnek szimmetriatengelye. Másrészt a $J M$ szakasz ugyanaz a szakasz a $K$ pont minden helyzeténél, mert $J$ kezdőpontja és $J M = K L$ hossza állandó, továbbá, ha az $e$ egyenesnek irányítást adunk, nem változik a $K L$ szakasznak ezzel az irányítással bezárt szöge, így a $J M$ szakasznak ezzel az iránnyal bezárt szöge, ami az előbbi szög kiegészítő szöge, szintén nem változik. Így $J M$ közös húrja az összes szóba jövő köröknek, tehát $f$ felező merőlegese átmegy a körök középpontjain.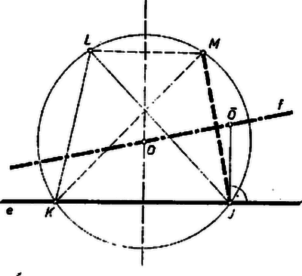

1. ábra

Legyen mármost

f

-nek egy tetszés szerinti pontja

O^{*}

és az

O^{*}

körül

O^{*} J

sugárral írt

k^{*}

kör második metszéspontja

e

-vel

K^{*}

, feltéve, hogy

k^{*}

nem érinti

e

-t. Legyen a

K^{*} J M

háromszög tükörképe

K^{*} J

felező merőlegesére

J K^{*} L^{*}

, akkor az előző meggondolás megfordításával adódik, hogy

K^{*} L^{*}

hossza és iránya a

K L

számára megadott távolság és irány, és a háromszög körülírt köre

k

. Így

O^{*}

pontja a mértani helynek.
Akkor kapunk

e

-t érintő kört, ha középpontnak az

e

-re

J

-ben állított merőlegesnek

f

-fel való

O

metszéspontját választjuk. Ekkor a

K^{*} M J

háromszög elfajul a

J M

egyenesszakasszá, s így

J K^{*} L^{*}

is egyenesszakasszá fajul. Tehát a mértani hely az

f

egyenes, az

O

pont kivételével.

Hirka András (Pannonhalma, Benedekrendi gimn. II. o. t.)

II. megoldás. Ha

K L

nem merőleges

e

-re, akkor válasszuk ki a szakasz két különleges helyzetét: 1. amikor a

J K L

háromszög

L

-nél derékszögű, ill. 2. amikor a háromszög egyenlő szárú:

J L = J K

(2. ábra). Csak egy-egy ilyen helyzet van, mindkettőt kitűzhetjük a

J

-ből

K L

irányára állított

h

merőlegessel. Arra az

L_{1}

pontra, amelyben

L

-nek

e_{1}

pályáját metszi

h, L_{1} K_{1} ⊥ J L_{1}

; ahol pedig a

K L

szakasz

F

felezőpontjának pályáját metszi, vagyis az

e

e_{1}

síksáv

t

szimmetriatengelyét, ott van a második helyzethez tartozó

F_{2}

, erre

F_{2} K_{2} ⊥ J F_{2}

. Legyenek a megfelelő körközéppontok

O_{1}

és

O_{2}

O_{1}

azonos

K_{2}

-vel, mert

F_{2} K_{2}

merőlegesen felezi a

J L_{1}

befogót, így felezi a

J K_{1}

átfogót is, és ez a felezőpont egyben a derékszögű háromszög köré írt kör középpontja. Másrészt

O_{2}

h

-n van. Megmutatjuk, hogy a mozgó szakasz tetszés szerinti

K L

helyzetéhez tartozó

O

középpont rajta van az

O_{1} O_{2}

egyenesen.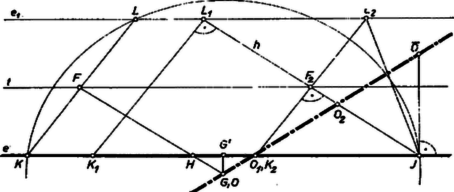

2. ábra

Messe a

K L

-re, ennek

F

felezőpontjában állított merőleges

O_{1} O_{2}

-t

G

-ben,

e

-t

H

-ban. Elegendő azt belátni, hogy

G

rajta van

J K

felező merőlegesén is. A

G H O_{1}

szög vagy azonos az

F H K

szöggel, vagy annak csúcsszöge, ezért egyenlő az utóbbival egyállású

F_{2} J K_{2}

szöggel. Viszont az

O_{2} J K_{2}

háromszög egyenlő szárú, így

F_{2} J K_{2} ∢ = O_{2} J K_{2} ∢ = O_{2} K_{2} J ∢ = O_{2} O_{1} J ∢

.Végül az

O_{2} O_{1} J

szög azonos a

G O_{1} H

szöggel, vagy annak csúcsszöge, így

G H O_{1} ∢ = G O_{1} J ∢ = G O_{1} H ∢

, és a

G H O_{1}

háromszög egyenlő szárú. Ezért,

G

-nek

e

-n levő vetületét

G'

-vel jelölve

H G'

és

O_{1} G'

egyenlő és ellentétes irányú szakaszok. ‐ Másrészt a

K F H

háromszög eltolással áll elő

K_{2} F_{2} J

-ből, ezért

H K

és

K_{2} J = O_{1} J

is egyenlő és ellentétes irányú szakaszok, ennélfogva ugyanez áll a

K G'

és

J G'

szakaszpárra. Ez pedig azt jelenti, hogy

G

rajta van

K J

felező merőlegesén is,

K L

-én is, vagyis

G

azonos a

J K L

háromszög köré írt kör

O

középpontjával. Ezt akartuk bizonyítani.
Azt, hogy az

O_{1} O_{2}

egyenes mely pontjai alkotják a mértani helyet, az I. megoldásban láttuk.
Ha

K L

merőleges

e

-re, akkor a

J K L

háromszög

K

-nál derékszögű, és

O

J L

átfogó felezőpontjában van. Másrészt

L

egy az

e

-vel párhuzamos

e_{1}

egyenest ír le, tehát a mértani hely az

e

e_{1}

egyenespárral határolt síksáv

t

szimmetriatengelye, kivéve

J

-nek

t

-re vett

\bar{O}

vetületét. Ebben az esetben

\bar{O}

is elfogadható, ha a

J L

szakasszá elfajult

J K L

háromszög körülírt körének azt a legkisebb sugarú kört tekintjük, amely átmegy

J

-n és

L

-en.

Radó Iván (Budapest, I. István g. I. o. t.)