Kezdőlap


Feladat:	761. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antal Magdolna , Berecz Ágota , Doskar Balázs , Ferenczi György , Gazsó János , Gecsey László , Gerencsér László , Horváth Péter , Huhn A. , Kiss Katalin , Leporisz Gy. , Lőrincz Cs. , Major P. , Malatinszky G. , Marosi Judit , Mayer János , Mészáros Gy. , Nagy Klára , Palotás Á. , Pázmányi Gy. , Raisz P. , Siket Aranka , Stiga Katalin , Szabó Mihály , Széchy G. , Szentai Judit , Szidarovszky Klára , Tamás E. , Tamás G. , Tóth L. , Török L. , Török László
Füzet:	1963/február, 59 - 62. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Tengelyes tükrözés, Körérintési szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1962/március: 761. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nyilvánvaló, hogy a szerkesztendő $k_{1}$ , $k_{2}$ , $k_{3}$ mindegyike az ívháromszög más két-két oldalát érinti. Középpontjuk: $O_{1}$ , $O_{2}$ , $O_{3}$ rendre az $A B C$ háromszög $B C$ , $C A$ , ill. $A B$ oldalának felező merőlegesén van, ugyanis pl. $B O_{1} = d - r = C O_{1}$ aho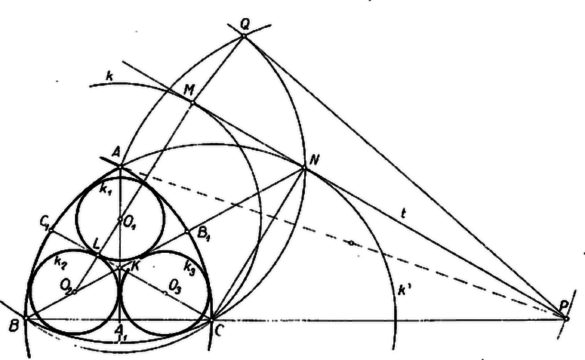l $r$ a $k_{1}$ sugara.
Legyen az $A B C$ háromszög középpontja $K$ és messék az $A K$ , $B K$ , $C K$ szimmetriatengelyek a $B C$ , $C A$ , $A B$ ívet $A_{1}$ -ben, $B_{1}$ -ben, ill. $C_{1}$ -ben. A $K B_{1} A C_{1}$ , $K C_{1} B A_{1}$ , $K A_{1} C B_{1}$ idomok egybevágók, mert egymásba átvihetők a tengelyeken való tükrözéssel. Kézenfekvő feltenni, hogy van olyan megoldás, melyben a keresett körök sorra e három idomba vannak beleírva, ezért sugaraik egyenlők, és így egymást páronként a $K C_{1}$ , $K A_{1}$ , ill. $K B_{1}$ szakaszon érintik; ezzel a többletkövetelménnyel fogunk megoldást keresni. (Kiegészítésül megmutatjuk majd, hogy más megoldás nincs, ha $k_{1}$ , $k_{2}$ , $k_{3}$ kívülről érintik egymást.)

1. ábra

Legyen

k_{1}

és

k_{2}

érintkezési pontja

L

, tekintsük az

O_{1}

körül

O_{1} B = d - r

sugarú

k

kört, és legyen ennek

L

-től távolabbi metszéspontja az

O_{1} O_{2}

egyenessel

M

. Így

L M = d

és

L M ⊥ C C_{1}

, mert

k_{1}

és

k_{2}

sugarainak egyenlőségéből

K O_{2} = K O_{1}

, és így

O_{1} O_{2} ⊥ C C_{1}

. Ha tehát vesszük az

A B

ívet tartalmazó

k'

körnek

C C_{1}

-gyel párhuzamos,

A

-hoz közelebbi

t

érintőjét és érintési pontját

N

-nel jelöljük, akkor az

N C L M

négyszög téglalap, és

t

k

-t is érinti

M

-ben. Ezért, a

B C

egyenes és

t

metszéspontját

P

-vel jelölve

P B \cdot P C = P M^{2}

. Ennek alapján

M

t

-n kijelölhető, és az

M

-en át

C C_{1}

-re állított merőleges kimetszi

K A

-ból

O_{1}

-et,

K B

-ből

O_{2}

-t,

O_{3}

-at pedig

O_{1}

-nek

B B_{1}

-re való tükrözésével kapjuk.
A

P M

szakasz hosszát megadja pl. a

P

-ből az ívháromszög

B C

oldalát tartalmazó körhöz szerkesztett érintő

P Q

hossza. (Jobb áttekinthetőség érdekében az ábrán a hosszabb

B C

ív érintője látható.) E szerkesztés végrehajtása mutatja, hogy van a többletkövetelményt is kielégítő megoldás.

Doskar Balázs (Budapest, Piarista g. II. o. t.)

Megjegyzések. 1.

t

-nek második olyan

M_{2}

pontjából, amelyre

P M_{2}^{2} = P Q^{2} = P B \cdot P C

, a fent leírt módon olyan három egyenlő sugarú, egymást páronként érintő kört kaphatunk, amelyek az

A

B

C

körül

d

sugárral írt körök közül (rendre más-más) kettőt kívülről érintenek.
2. Megmutatjuk, hogy a megszerkesztett körhármason kívül a feladatnak nincs más megoldása, ha csak egymást kívülről érintő köröket engedünk meg. Nem lehet, hogy mindhárom kör az ívháromszögnek ugyanazt a két oldalát érintse, mert ha az

r_{1}

r_{2}

r_{3}

sugarú körök egymást páronként kívülről érintik, akkor középpontjaik távolságai:

r_{1} + r_{2}

r_{2} + r_{3}

r_{3} + r_{1}

eleget tesznek a háromszög egyenlőtlenségnek, tehát a középpontok háromszöget alkotnak, holott egy egyenesen kellene lenniök, a két kiszemelt ív szimmetriatengelyén.
Nem lehet pl. az

A B

és

A C

oldalakat érintő

k_{1}

kör

O_{1}

középpontja a

K A_{1}

szakaszon, mert így sugarára

r_{1} = d - B O_{1} > d - B K = B_{1} K = K A_{1} > O_{1} A_{1}

tehát

A_{1}

k_{1}

belsejében van, a

k_{2}

-t és

k_{3}

-at magukba foglaló ívháromszögeknek (2. ábra, egy-egy csúcsuk

B

, ill.

C

) nincs közös pontjuk,

k_{2}

és

k_{3}

nem érintkezhetnek.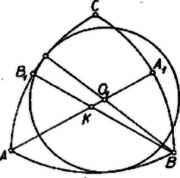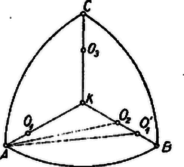

2. ábra

3. ábra

Tegyük fel mármost, hogy

k_{1}

k_{2}

k_{3}

megoldást adnak,

O_{1}

O_{2}

O_{3}

rendre a

K A

K B

K C

szakaszon van, és

K O_{1} > K O_{2}

(3. ábra). Ekkor

O_{1}

-nek

C K

-ra vett

O'_{1}

tükörképe a

K O_{2}

szakasz

O_{2}

-n túli meghosszabbításán van. A

K O_{2} A

szög hegyesszög, mert

A K O_{2} ∢ = 120^{\circ}

. Ezért az

O'_{1} O_{2} A

háromszögben

O_{2}

-nél tompaszög van, tehát

A O'_{1} > A O_{2}

, és így

k_{1}

és

k_{2}

sugarára

\begin{matrix} r_{1} = d - B O_{1} = d - A O'_{1} < d - A O_{2} = r_{2} . \end{matrix}

(1)

Másrészt hasonlóan

O_{3} O_{2} < O_{3} O'_{1} = O_{3} O_{1}

, azaz (

k_{3}

sugarát

r_{3}

-mal jelölve)

\begin{matrix} r_{3} + r_{2} < r_{3} + r_{1}, amiből r_{2} < r_{1}, \end{matrix}

ellentétben (1)-gyel. Ugyanígy

K O_{1} < K O_{2}

is ellentmondásra vezet, tehát

K O_{1} = K O_{2}

, és

r_{1} = r_{2}

. Ezt akartuk bebizonyítani.
3. A szerkesztendő körök között belső érintkezést is megengedve a fenti megoldásból leszármaztathatunk olyan három egymást páronként érintő kört, melyek mindegyike belülről érinti az ívháromszög más két-két oldalát, azonban e körök egyike részben kívül van az ív háromszögön:

k_{1}

-et és

k_{2}

-t meghagyva vegyük

k'_{3}

középpontjának az

A O_{2}

és

B O_{1}

egyenesek

O'_{3}

metszéspontját (4. ábra).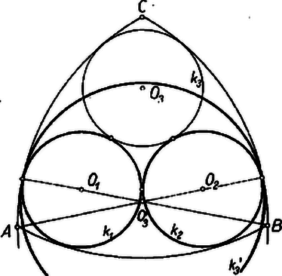

4. ábra

A megoldók nagy része az érintő körök sugarának kiszámításán keresztül adott meg szerkesztési eljárást. Egy ilyen megoldás a következő:
II. megoldás. Az I. megoldás többletkövetelményét fenntartva kiszámítjuk a három kör közös

r

sugarát. Az

O_{1} C L

derékszögű háromszögben

O_{1} L = r

O_{1} C = d - r

és

C L = C K + K L

(1. ábra). Itt

C K

A B C

háromszög

d \sqrt[]{3} / 2

súlyvonalának

2 / 3

része:

d / \sqrt[]{3}

K L

pedig egyenlő az

r

magasságú szabályos háromszög oldalának felével,

r / \sqrt[]{3}

-mal, mert

O_{1} K L ∢ = 60^{\circ}

. Így Pythagorász tételével

\begin{matrix} {(d - r)}^{2} = r^{2} + {(\frac{d + r}{\sqrt[]{3}})}^{2}, r^{2} + 8 d r - 2 d^{2} = 0, \end{matrix}

és ennek pozitív gyöke:

\begin{matrix} r = d (3 \sqrt[]{2} - 4) . \end{matrix}

(2)

r

megszerkeszthető, ebből

d - r

is, és ekkor a

B

és

C

körül

d - r

sugárral írt köröknek az ívháromszögben levő metszéspontja

O_{1}

O_{2}

-t és

O_{3}

-at megfelelő tükrözéssel kapjuk.

r

szerkesztésére egy lehetőség:

d

oldalú négyzet átlójának 3-szorosából kivonjuk az oldal 4-szeresét.
Eredményünk helyességének bizonyításául csak azt kell megmutatnunk, hogy a (2) érték mellett az

O_{1} C L

háromszög oldalaira felhasznált kifejezések pozitívok.

r > 0

, mert

3 \sqrt[]{2} = \sqrt[]{18} > 4

, így

d + r > 0

is fennáll. Végül

d - r = d (5 - 3 \sqrt[]{2}) > 0

, mert

\sqrt[]{18} < 5

Antal Magdolna (Budapest, Varga K. lg. II. o. t.)
Gazsó János (Szeged, Ságvári E. gyak. g. II. o. t.)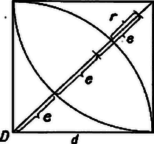

5. ábra

Megjegyzés. Kevesebb helyet igényel

r

szerkesztése a következő módon (5. ábra). Írjunk a

d

oldalú négyzetbe

D

csúcsa mint középpont körül

d

sugarú negyedkört, húzzuk meg

D

-ből az átlót és mérjük fel az átlónak a körön kívüli

e

szakaszát

D

-ból kiindulva az átlóra 3-szor egymás után. Ekkor a harmadik szakasz végpontjának a körívtől való távolsága

3 d (\sqrt[]{2} - 1) - d = d (3 \sqrt[]{2} - 4) = r

Berecz Ágota (Makó, József A. g. II. o. t.)