Feladat: 759. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Czina Ferenc ,  Kobzos László 
Füzet: 1962/november, 152 - 155. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek egybevágósága, Pont körüli forgatás, Síkgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1962/március: 759. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) A négyzet középpontja felezi az átlókat, ezért a kérdéses O1LO2K=S négyszög csúcsai felezik az AMPC=T négyszög oldalait (1. ábra). Így O1L az APM háromszögnek AP-vel párhuzamos középvonala, O1L=AP/2. Hasonlóan az APC háromszögből KO2∥AP és KO2=AP/2, és így O1L#KO2. Ugyanígy O1K#LO2, ezek szerint S paralelogramma.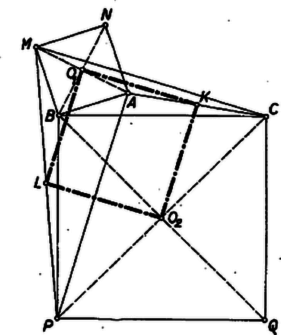

 
 
1. ábra
 

S akkor és csak akkor négyzet, ha két szomszédos oldala merőleges és egyenlő hosszú. Elég azt belátnunk, hogy T-nek AP és MC átlói merőlegesek és egyenlők. Végpontjaikhoz a B csúcsot hozzávéve az ABP és MBC háromszögek egybevágók, mert B körül 90∘-kal elforgatva az egyik a másikba vihető át. Valóban a négyzetek ‐ ABMN és PBCQ ‐ körüljárása megegyezik, így BA ugyanolyan irányú, B körüli, 90∘-os elforgatással vihető át BM-be, mint BP BC-be, ez az elforgatás tehát a ABP háromszöget MBC-be viszi át. Ez abban az esetben is érvényes, ha ABC∢=90∘, s így az ABP és MBC háromszögek egyenesszakasszá fajulnak. Az AP és MC szakaszok eszerint merőlegesek és egyenlők, mert egy alkalmas, 90∘-os elforgatás az előbbit az utóbbiba viszi át. Ebből, mint láttuk, következik a feladat a) részének állítása.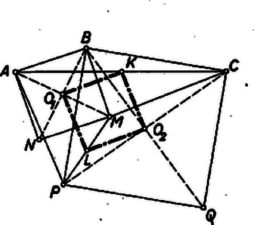
 
 
2. ábra
 

A bizonyítás egyaránt érvényes, ha az ABC háromszög B-nél levő szöge hegyes-, derék-, vagy tompaszög, továbbá akár ,,kifelé'', akár ,,befelé'' (az oldalegyenesnek a háromszöget nem tartalmazó, ill. az azt tartalmazó partján, 2. ábra) rajzoltuk a négyzeteket; az utóbbi esetben azonban, ha az ABC háromszög B-nél derékszögű, továbbá egyenlő szárú, akkor S négy csúcsa egybeesik.
b) Legyen ABCDEF=H1 egy centrálisan szimmetrikus hatszög, legyenek az előírt szabályos háromszögek BAI, CBJ, DCK, EDL, FEM, AFN, végül az IJKLMN hatszög egymás utáni oldalainak felezőpontjai P, Q, R, S, T, U (3. ábra). Megmutatjuk, hogy a PQRSTU=H2 hatszög bármelyik oldalegyenesét egy‐egy (alkalmas középpont körüli) azonos irányú, 60∘-os forgatással át lehet vinni a következőbe. Ebből a b) állítás következik. Ugyanis a szabályos hatszög külső szöge 60∘, ennyi az irányváltozás, ha a hatszög körüljárása során egy oldal irányából átfordulunk a következő oldal irányába. Konkrétan azt fogjuk bizonyítani, hogy QR=PQ. E két oldal a KJL háromszögnek JL-lel, ill. a JIK-nak IK-val párhuzamos középvonala, ezért a JL=IK egyenlőséget mutatjuk meg, továbbá azt, hogy IK-t a JL-lel párhuzamos helyzetbe egy 60∘-os forgás viszi át.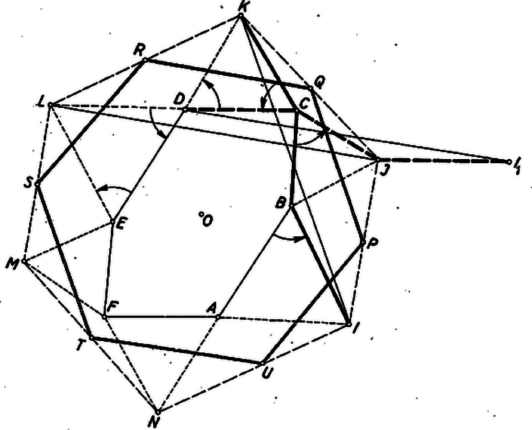
 
 
3. ábra
 

Forgassuk el a KCBI törött vonalat C körül 60∘-kal abban az irányban, hogy B a J-be jusson. Ekkor K a D-be fordul, I új helyzete pedig legyen I1. A DLJI1 idom paralelogramma, mert egyrészt DL=DE=BA=BI=JI1, másrészt a DL, JI1 szakaszok párhuzamosak és ellentétes irányúak, ugyanis DL irányából DE és BA, majd BI, végül JI1 irányába három ugyanazon irányú, 60∘-os forgással jutunk át, vagyis összesen 180∘-os forgással. Ezért JL=I1D=IK, és IK, vagy a vele párhuzamos PQ irányából valóban 60∘-os forgással jutottunk át I1D, JL és QR közös irányába.
A felhasznált 60∘-os forgások irányának megegyezése abból következik, hogy H1 oldalaira a szabályos háromszögeket mindig kifelé szerkesztettük, és így a BAI, CBJ, DCK, EDL háromszögek most felsorolt körüljárási irányai egyezők. Ezért első forgatásunkban a KCD forgásszög iránya egyező a CDK és tovább a BCJ forgásszög irányával (a 3. ábrán a forgások pozitívok) ‐ mint állítottuk ‐, és ugyanilyen irányúak az LDE és az ABI forgások.
A fenti bizonyításban csak 4, a H1-nek egymás utáni oldalaira rajzolt egyenlő oldalú háromszöget használtunk fel, továbbá H1 centrálisan szimmetrikus voltából csupán BA és DE párhuzamosságát és egyenlőségét. A feltevés fel nem használt részei H2 további RS, ST, TU, UP oldalai egyenlőségének bizonyításához szükségesek, valamint ahhoz, hogy a többi külső szögek is 60∘-osak és ugyanolyan forgási irányúak.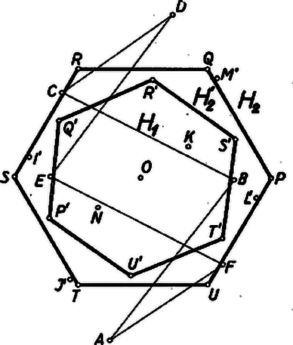
 
 Czina Ferenc (Makó, József A. g. I. o. t.)

 
 
4. ábra
 

Megjegyzés. A 3. ábrán H1 konvex, de e tulajdonságát nem használtuk fel; ezért bizonyításunk ‐ a követelménynek megfelelően ‐ tetszés szerinti centrálisan szimmetrikus hatszögre érvényes. A 4. ábrán H1 hurkolt, itt a szabályos háromszögek ,,kifelé'' való rajzolásának már nincs értelme, mert H1-nek 4 olyan oldala van, amelyhez képest a többi csúcsok kétoldalt helyezkednek el. Az AB oldalhoz képest a szimmetriacentrummal ellentétes partot vettük külsőnek, tovább pedig úgy haladtunk, hogy a BAI, ..., AFN háromszögek egyenlő körüljárásúak legyenek. Fel van tüntetve az oldalak másik partján szerkesztett ABI', ..., FAN' szabályos háromszögekből adódó P'Q'R'S'T'U' hatszög is, ‐ hiszen AB-nek másik partját is vehettük volna külsőnek. A bizonyításból nyilvánvaló, hogy ez is szabályos, valamint az is, hogy nem hurkolt H1 oldalaira mindig befelé rajzolt szabályos háromszögekből kiindulva is igaz az állítás, hacsak a P, ..., U pontok nem esnek egybe. Az így adódó H2' a H2 höz képest mindig ellentétes körüljárású.
 
II. megoldás a b) részre. A következőkben csak vázoljuk egy második megoldás gondolatmenetét, nem elemezve, hogyan módosul az az ábrától különböző viszonyok (pl. konkáv vagy hurkolt hatszög) esetén.
Elég megmutatnunk, hogy pl. OPQ szabályos háromszög ‐ ahol O a H1 középpontja ‐, mert akkor ugyanez áll az OQR, ORS, OST, OTU, OUP háromszögekre is, s így PQRSTU szabályos hatszög. A P, Q pontok megszerkesztésében viszont csak az AB, BC, CD oldalak fölé rajzolt szabályos háromszögeknek van szerepe.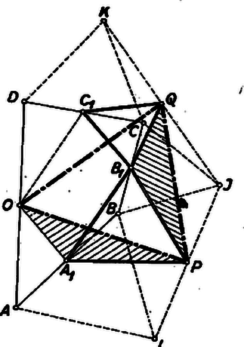
 
 
5. ábra
 

Tekintsük tehát az ábrának csak az ABCD négyszög meghatározta részét (5. ábra). Itt O az AD oldal középpontja. Ha még berajzoljuk az AB, BC, CD oldalak A1, B1, C1 felezőpontját, akkor az A1PB1, B1QC1 háromszögek szabályosnak látszanak. Megmutatjuk, hogy valóban szabályos háromszögek. A két háromszög hasonló módon keletkezik az IBJ, ill. JCK háromszögből. Az állítást a következő segédtétel fejezi ki:
Rajzoljunk egy V1V2V3 háromszög V2V3 és V3V1 oldalára kifelé V2V3X és V3V1Y szabályos háromszögeket (6. ábra). Ekkor a V1V2, V3X és V3Y szakaszok W, Z1 és Z2 felezőpontjai egy szabályos háromszög csúcsai.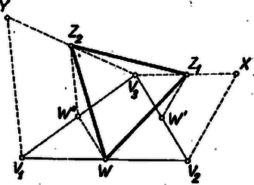
 
 
6. ábra
 

Jelöljük még a V2V3 és V3V1 oldalak felezőpontjait W', W''-vel. Ekkor V3Z2W'' szabályos háromszög. Forgassuk el Z2 körül a Z2W''W háromszöget 60∘-kal úgy, hogy W'' a V3 pontba menjen át. Ekkor W elforgatás után Z1-be kerül, mert mint középvonal W''W#V3W', másrészt Z1V3W' szabályos háromszög, tehát Z1V3 egyenlő W''W-vel és irányaik a kívánt irányban 60∘-os szöget zárnak be. Az elforgatás így Z2W-t Z2Z1 be viszi át, a két szakasz tehát egyenlő és 60∘-os szöget zár be, vagyis a Z1Z2W háromszög szabályos.
A segédtételt V1V2V3 helyett IJB-re, ill. JKC-re alkalmazva nyerjük, hogy az A1B1P és B1C1Q háromszögek valóban szabályosak.
Az OPQ háromszög szabályos voltának megmutatásához forgassuk most el a PA1O háromszöget P körül 60∘-kal úgy, hogy A1 a B1-be jusson. A1OC1B1 paralelogramma, így A1O#B1C1; mivel továbbá C1B1Q szabályos háromszög, így A1O és B1Q iránya 60∘-os szöget zár be, a PA1O háromszög elforgatás után tehát PB1Q-t fedi. Eszerint PO és PQ egyenlő és 60∘-os szöget zár be, tehát POQ szabályos háromszög.
Mint láttuk, ebből következik a feladat b) részének állítása.
 
 Kobzos László (Vác, Lőwy S. gépip. t. II. o. t.)
 
Megjegyzés. Néhányan vektorok felhasználásával bizonyították az állításokat, vagy a komplex számsíkon végzett számításokkal.