Feladat: 750. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Corradi Gábor ,  Gecsey László ,  Horváth Péter 
Füzet: 1962/november, 146 - 148. oldal  PDF  |  MathML 
Témakör(ök): Mértani helyek, Terület, felszín, Gyakorlat
Hivatkozás(ok):Feladatok: 1962/január: 750. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Egyelőre csak az ABCD=N négyszög belsejében keressük az előírt tulajdonságú pontokat. Ekkor O benne van a BDA és BDC háromszögek egyikében, legyen a betűzés olyan, hogy a BDA△-ben. Így az OBCD négyszög területe egyenlő a BDC és BDO háromszögek területének összegével, az OBAD négyszögé pedig a BDA és BDO háromszögek területének különbségével, mert ez a négyszög konkáv. A területeket ugyanúgy jelölve, mint magukat az idomokat, az OBCD=OBAD követelményből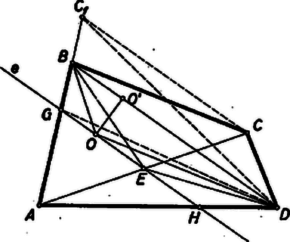

BDC+BDO=BDA-BDO, és ígyBDO=BDA-BDC2.



 
 
1. ábra
 

A BDO háromszög területe tehát az O pont minden helyzetére ugyanaz az érték kell, hogy legyen. Állandó a BD oldal is, tehát az O pontból erre bocsátott OO' magasság is állandó kell, hogy legyen O minden helyzeténél, tehát minden megfelelő O pont rajta van egy a BD-vel párhuzamos e egyenesen.
Az AC átló E felezőpontja hozzátartozik a mértani helyhez. Ugyanis az ABE és EBC háromszögek AE és EC oldala egyenlő, az ezekre B-ből bocsátott magasság közös, tehát területük egyenlő. Ugyanígy látható, hogy AED=ECD. Mivel pedig N konvex, így E a belsejében van, és az ABED négyszög az ABE és AED háromszög összege, a BCDE négyszög pedig a BCE és CDE háromszögeké, területük tehát valóban egyenlő. ‐ Eszerint e az E-n át a BD átlóval párhuzamosan húzott egyenes, O az e-nek csak az N-be eső GH szakaszán lehet (G az AB-n van, H az AD-n).
Ha a GH szakasz egy tetszés szerinti belső pontja O*, akkor O*BAD=ABD-O*BD, és ez O* megválasztása szerint egyenlő EBAD=EBCD=O*BCD-vel, tehát O* beletartozik a mértani helybe. G-t véve O gyanánt, a GBAD négyszög elfajult, területe annyi, mint a GAD háromszögé; de így is egyenlő GBCD területével. Eszerint G tágabb értelemben szintén hozzátartozik a mértani helyhez és ugyanez áll H-ra is.
N-en kívül nincs az OBAD=OBCD követelménynek megfelelő O pont. Ha ugyanis az A, vagy a C szög csúcsszögtartományának egy pontja P (2. ábra I és III síkrésze), akkor a PBAD és PBCD négyszögek egyike éppen N területével nagyobb a másiknál, nem egyenlők. A sík H részében vett P-vel a PD szakasz átmetszi az AB és BC szakaszok egyikét, a IV-ben pedig PB szakasz metszi az AD és DC szakaszok egyikét, ezért a PBAD és PBCD négyszögek egyike hurkolt, az ilyenek területét viszont nem értelmeztük.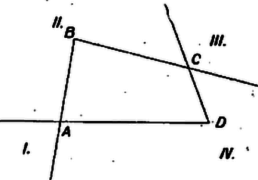
 
 
2. ábra
 

Ezek szerint a keresett mértani hely a BD átlóval az AC átló felezőpontján át húzott párhuzamosnak N-be eső szakasza, végpontjait csak tágabb értelemben megengedve. Ha BD felezi AC-t, akkor a mértani hely csak tágabb értelemben létezik ‐ maga a BD szakasz az ‐, mert az OBAD és OBCD négyszögek elfajulnak háromszöggé.
 
II. Eredményünkből ‐ az A, B, valamint C, D betűk felcserélésével következik, hogy az OABC=OCDA követelményt kielégítő O pontok mértani helye az AC átlóval a BD átló F felezőpontján át húzott f párhuzamosnak N-be eső JK szakasza, a végpontokat csak tágabb értelemben engedve meg. (Ha AC felezi BD-t, akkor JK≡AC, és az OABC, OCDA négyszögek elfajulnak.) Ennélfogva a keresett O pont csak e és f metszéspontja lehet, de csak akkor felel meg, ha N belsejében van. Megmutatjuk, hogy ez mindig teljesül.
E közelebb van az átlók M metszéspontjához, mint A-hoz, mert feltevésünk mellett BD ugyanazon partján van, mint A, így pedig AE=EC=EM+MC>EM. Hasonlóan kapjuk ‐ olyan betűzést használva, amely mellett B távolabb van AC-től, mint D ‐, hogy F közelebb van M-hez, mint B-hez. Így az MEOF paralelogramma benne van az MRSQ paralelogrammában ‐ ahol Q, R, S az ABM háromszög oldalfelező pontjai ‐, tehát O benne van az ABM háromszögben, amely része N-nek. Ha pedig egyik, vagy mindkét átló felezi a másikat, akkor e és f metszéspontja a másikat felező átló felezőpontja, tehát N-ben van. Ezzel a megoldást befejeztük.
 
 Gecsey László (Budapest, József A. g. II. o. t.)
 Horváth Péter (Budapest, Kossuth L. gépip. t. II. o. t.)
 Corradi Gábor (Győr, Czuczor G. g. II. o. t.)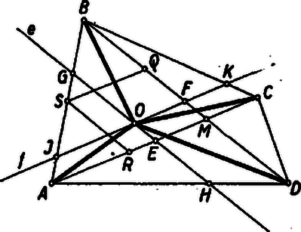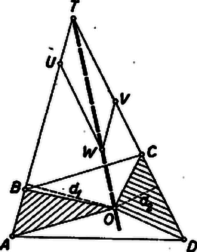
 
Megjegyzések. 1. Az e egyenest az E pont felhasználása nélkül is megkaphatjuk. Messe a BD-vel párhuzamos, C-n átmenő egyenes AB-t C1-ben (1. ábra), ekkor az AC1 szakasz felezőpontja G. Erre abból is rájöhetünk, hogy OBCD=OBAD-ből OBCD=N/2, és ekkora terület kijelölése céljára előkészítésül N helyett a vele egyenlő területű AC1D háromszöget is felezhetjük DG-vel.
 
 Horváth Péter
 
 
3. ábra
 
 
4. ábra
 


2. A feladat II. részében keresett O pontot az I. részben megállapított helyett más mértani hely felhasználásával is megkaphatjuk. OABC=OBCD-ből az OBC közös rész elhagyásával OAB=OCD, ezért O-nak AB és CD-től való d1, ill. d2 távolságára d1:d2=CD:AB. Könnyű belátni, hogy eszerint O mértani helye egy az AB és CD egyenesek T metszéspontján átmenő egyenes, és ennek egy további W pontját úgy kapjuk, ha felmérjük TA-ra a TU=AB szakaszt, TC-re a TV=CD szakaszt és megszerkesztjük az UTVW paralelogrammát. Még egy egyenest kapunk O-ra OBC=ODA-ból, a kettő metszéspontja a keresett O.
 
3. A hurkolt négyszög területén az oldalak által körülhatárolt két háromszög területének összegét értve Gecsey László és Horváth Péter az N-en kívül is találtak O pontokat: így a DG egyenes G-ből kiinduló, D-t nem tartalmazó félegyenesének minden pontja megfelel, továbbá a BH egyenes H-ból kiinduló, B-t nem tartalmazó félegyenesének minden pontja.
Megjegyezzük, hogy célszerűbb hurkolt idomok területét úgy értelmezni, hogy az egyes körüljárt részidomok területét előjellel vesszük aszerint, hogy a hurkolt idom határát egyszer végigjárva a részidom határoló vonalán milyen körüljárási irány szerint haladtunk végig.