Kezdőlap


Feladat:	746. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bulkai Lajos , Corradi Gábor
Füzet:	1962/november, 142 - 144. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Kör (és részhalmaza), mint mértani hely, Húrnégyszögek, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1962/január: 746. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $P$ -hez rendelt $k_{1}$ és $k_{2}$ körök középpontját vehetjük az $A B$ egyenessel kettévágott sík ugyanazon félsíkján, vagy a két különböző félsíkon (magán az $A B$ szakaszon nem, mert $λ > 1 / 2$ , és így a középpontok $A P$ -vel, ill. $P B$ -vel valóságos háromszöget alkotnak). Tekintsük előbb az első lehetőséget. Legyen a két középpont $O_{1}$ és $O_{2}$ az $F'$ félsíkon úgy, hogy $0_{1} A = O_{1} P = λ \cdot A P$ és $O_{2} B = O_{2} P = λ \cdot B P$ , és a körök második közös pontja $M$ (első közös pontnak $P$ -t véve). Az $A P O_{1}$ és $P B O_{2} △$ -ek hasonlók, mert az egymás utáni oldalak aránya mindkettőben $1 : λ : λ$ ; ezért $A O_{1} P ∢ = P O_{2} B ∢$ . Ez a szög független $P$ helyzetétől, csak $λ$ értékétől függ; jelöljük a nagyságát $ω$ -val. $A M P$ az első körben a rövidebb (az $F''$ -beli) $A P$ íven nyugvó kerületi szög, ugyanígy a $P M B$ szög a második kör $F''$ -beli $P B$ ívén (mert $M$ ugyancsak $F'$ -n van, ugyanis $M$ a $P$ -nek tükörképe az $O_{1} O_{2}$ egyenesre). Ezért $A M P ∢ = P M B ∢ = ω / 2$ , és $A M B ∢ = A M P ∢ + P M B ∢ = ω$ , állandó, tehát $M$ csak azon az ( $F'$ -beli) $i'$ köríven lehet, amelynek pontjaiból az $A B$ szakasz $ω$ szögben látszik.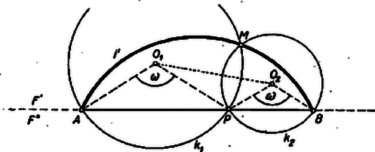

1. ábra

Ha már most

M^{*}

i'

-nek tetszés szerinti,

A

-tól és

B

-től különböző pontja, akkor létezik olyan

P^{*}

pont, amelyhez a feladat előírása szerint éppen

M^{*}

tartozik hozzá, éspedig

P^{*}

-ot az

A M^{*} B

szög felezője metszi ki

A B

-ből. Így ugyanis

A M^{*} P^{*} ∢ = P^{*} M^{*} B ∢ = ω / 2

, tehát

M^{*}

rajta van a

P^{*}

-hoz hozzárendelt körökön (továbbá különbözik

P^{*}

-tól, másrészt

P^{*}

A B

szakasz belsejében van). Ha

M

A

-ban vagy a

B

-ben volna,

P^{*}

egybeesnék

A

-val, ill.

B

-vel, így viszont az

M

-et meghatározó körök egyike nem jönne létre.
Ezek szerint az

i'

ív belseje része a keresett mértani helynek; és nyilván ugyanez áll

i'

-nek

A B

-re vett

i''

tükörképére is. Ezt akkor kapjuk, ha a

P

-hez hozzárendelt körök középpontjait

F''

-ben vesszük fel.
Végül ha

O_{1}

F'

-n,

O_{2}

pedig

F''

-n van, az utóbbit jelöljük

O_{2}''

-vel, akkor

O''_{2}

nyilván mindig a fenti

O_{2}

-nek

A B

-re vett tükörképe. Így

O''_{2}

P

és

O_{1}

egy egyenesbe esnek, mert a tükrözés, valamint az

A P O_{1}

és

B P O_{2}

egyenlő szárú háromszögek hasonlósága miatt

O''_{2} P B ∢ = O_{2} P B ∢ = O_{1} P A ∢

, tehát a

P

-höz rendelt két kör érinti egymást. Ezért második közös pontjuk is maga

P

.
Mindezek szerint a keresett mértani hely az

i'

i''

körívekből és az

A B

szakaszból áll,

A

-t,

B

-t nem hozzászámítva.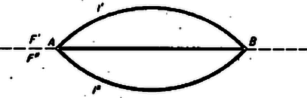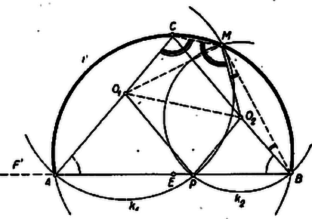

2. ábra

Bulkai Lajos (Győr, Czuczor G. g. I. o. t.)

II. megoldás. Csak az

F'

-beli

M

pontok mértani helyét vizsgáljuk. Az I. megoldásbeli

ω

szög állandósága folytán az

O_{1} A B

és

O_{2} B A

szögek is állandók, tehát

O_{1}

és

O_{2}

P

minden helyzetében annak az

A B C

egyenlő szárú háromszögnek a szárain vannak, amelyre

A C = B C = λ \cdot A B

és

A C B ∢ = ω

, mégpedig úgy, hagy

P O_{1} ∥ B C

P O_{2} ∥ A C

. Megmutatjuk, hogy

M

mindig rajta van az

A B C △

körülírt körének

F'

-beli ívén. A szimmetria miatt szorítkozhatunk az

E B

szakaszon levő pontokra, ahol

E

A B

szakasz felezőpontja.

3. ábra

P \equiv E

, akkor nyilván

M \equiv C

. ‐ Az

O_{1} P O_{2} C

idom mindig paralelogramma, ezért az

O_{1} O_{2} C △

egybevágó és azonos körüljárású

O_{2} O_{1} P

-vel, ez pedig egybevágó és ellentétes körüljárású

O_{2} O_{1} M

-mel, mert

M

P

tükörképe

O_{1} O_{2}

-re. Ezért

O_{1} O_{2} C

és

O_{2} O_{1} M

egymás tükörképei

O_{1} O_{2}

felező merőlegesére, tehát

O_{1} O_{2} M C

egyenlő szárú (húr-) trapéz és

O_{2} M C ∢ = O_{1} C M ∢

. Így az

A B M C

négyszög

A

és

M

csúcsainál levő szögek összege:

\begin{matrix} B A C ∢ + B M C ∢ = A B C ∢ + (B M O_{2} ∢ + O_{2} M C ∢) = (A B C ∢ + O_{2} B M ∢) + \\ + O_{1} C M = A B M ∢ + A C M ∢, \end{matrix}

egyenlő a

B

és

C

csúcsoknál levő szögek összegével, tehát a négyszög húrnégyszög. Ezzel állításunkat bebizonyítottuk.
Megfordítva: az

A B C △

köré írt kör

A

-t nem tartalmazó

B C

ívén felvett tetszés szerinti

M^{*}

-hoz úgy kapjuk az őt előállító

P^{*}

pontot, mint a

B M^{*}

felező merőlegesével

B C

-ből kimetszett

O_{2}^{*}

pont körül

O_{2}^{*} B = O_{2}^{*} M^{*}

sugárral írt

k_{2}^{*}

körnek

A B

-vel való második metszéspontját. Így a

P^{*} B O_{2}

egyenlő szárú háromszög hasonló

A B C △

-höz, mert

B

-nél levő szögük közös, ezért

O_{2}^{*} P^{*} = λ \cdot P^{*} B

, vagyis

O_{2}^{*}

azonos a

P^{*}

-hoz rendelt

O_{2}

-vel,

k_{2}^{*}

azonos

k_{2}

-vel, tehát

k_{2}

valóban átmegy

M^{*}

-on; továbbá

P^{*} O_{2} ∥ A C

. A

P^{*}

-hoz rendelt

O_{1}

-et

A C

-ből a

P^{*}

-on átmenő,

B C

-vel párhuzamos metszi ki, és csak azt kell belátnunk, hogy az

O_{1}

körül

O_{1} P

sugárral írt kör átmegy

M^{*}

-on.

M^{*}

felvétele folytán

B A C ∢ + B M^{*} C ∢ = A B M^{*} ∢ + A C M^{*} ∢

. Vonjuk ki ebből a feltevés és

O_{2}

szerkesztése folytán fennálló

B A C ∢ + B M^{*} O_{2} ∢ = A B C ∢ + O_{2} B M^{*} ∢ = A B M^{*} ∢

egyenlőséget, nyerjük:

O_{2} M^{*} C ∢ = A C M^{*} ∢ = O_{1} C M^{*} ∢

. Másrészt szerkesztésnél fogva

C O_{1} = O_{2} P^{*} = O_{2} M^{*}

, tehát a

C M^{*} O_{1}

és

M^{*} C O_{2}

háromszögek egybevágók, mert a

C

-ben, ill.

M^{*}

-ban levő szögeik és itt összefutó oldalaik egyenlők. Ezért

O_{1} M^{*}

egyenlő

O_{2} C

-ve1, ez pedig szerkesztésnél fogva

P^{*} O_{1}

-gyel,

k_{1}

sugarával, tehát

k_{1}

valóban átmegy

M^{*}

-on.
Eszerint

M

mértani helye (

F'

-ben) az

A B

szakasz

A M B ∢ = A C B ∢ = ω

nyílású látószögköríve.

Corradi Gábor (Győr, Czuczor G. g. II..o. t.)

Megjegyzés. A fentiek alapján

C O_{1} + C O_{2} = C A

, állandó, és

M

-et így is származtathatjuk: egy

A B C

egyenlő szárú háromszög (

A C = B C

)

A C

és

B C

szárán legyen

O_{1}

és

O_{2}

úgy, hogy

O_{1} C + C O_{2} = A C

. Ekkor

M

O_{1} C O_{2}

háromszög köré írt kör második közös pontja a

C

-n átmenő,

O_{1} O_{2}

-vel párhuzamos egyenessel. Így a feladat az 1961. évi Arany Dániel tanulóversenyek haladó fokán a II. fordulóban kitűzött 3. feladat¹ általánosítása arra az esetre, ha derékszög helyett a

λ

-val meghatározott

A C B

szögből indulunk ki.

λ = 1 / \sqrt[]{2}

esetén az

A C B

szög derékszög.
Corradi Gábor

¹Lásd K. M. L. 24 (1962/1) 11. o.