Feladat: 745. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Somos Péter ,  Szentai Judit 
Füzet: 1962/november, 140 - 142. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Súlypont, Magasságpont, Körülírt kör középpontja, Terület, felszín, Gyakorlat
Hivatkozás(ok):Feladatok: 1962/január: 745. matematika gyakorlat

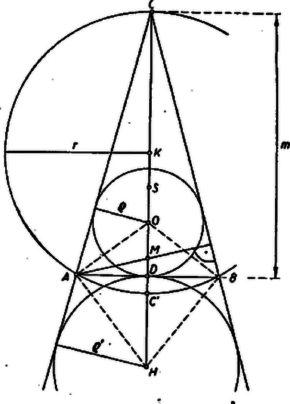
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Mindegyik vizsgálandó nevezetes pont a háromszög tengelyén van. A köztük levő távolságok legfeljebb 0,2 mm pontosságig mérhetők meg, ha ti. a szerkesztést jól hegyezett kemény ceruzával végeztük, amely kb. 0,1 mm vastag vonalat rajzol. (A több lépésből álló szerkesztésekben az elkerülhetetlen hibák felszaporodhatnak; ezért is célszerű a szerkesztést ‐ ha csak mérésre szorítkozunk ‐ legalább kétszer, egymástól függetlenül elvégezni.) A pontokat a feladat fenti sorrendjében S, M, K, 0, H-val jelölve a távolságokat (mm-ben) az alábbi táblázat tünteti fel (a teljes táblázat a jobbra lejtő átlóra szimmetrikus lenne, elég a felét kiírni):

 
|S-igO-igM-igH-ig|K-tól15,531,046,593,0|S-től-15,531,077,5|O-tól--15,562,0|M-től---46,5

 
 

Érdekes, hogy a 15,5 mm mérési eredmény 3-szor, a 31,0 és 46,5 mm pedig 2-szer‐2-szer lép fel, továbbá, hogy a 31,0, 46,5, 62,0, 77,5, 93,0 mm-es eredmény a 15,5-nek rendre 2-szerese, ill. 3-, 4-, 5-, 6-szorosa.
 
 Szentai Judit (Budapest, Kanizsay D. lg. I. o. t.)
 Treer Mária (Budapest, Kaffka M. lg. I. o. t.)
 
II. A távolságokat számítással pontosan megállapíthatjuk. Legyenek a háromszög csúcsai A, B, C, ahol AB=60 mm, és az alap felezőpontja D. Ekkor az ACD derékszögű háromszögből a magasság m=CD=13500=3013 mm (tovább is a mm az egység), DS=CD/3=1015, mert S harmadolja DC-t. Az AMD és CBD derékszögű háromszögek hasonlók, mert A és C-nél levő (hegyes) szögeik szárai páronként merőlegesek, ezért
DM=DADC⋅DB=215.
Legyen a körülírt kör sugara r, a C-vel átellenes pontja C'. Így a CC'A derékszögű háromszögből az ismert mértani középarányos tétel szerint
CA2=CD⋅CC'=2r⋅CD,r=1615,és így DK=m-r=1415.


O és H helyzetének meghatározására kiszámítjuk D-től való távolságukat. Ezek egyenlők a beírt kör ϱ, ill. a hozzáírt kör ϱ' sugarával, mert a körök AB-t éppen D-ben érintik. ϱ-t meghatározhatjuk abból, hogy ϱ az ABO, BCO és CAO háromszögeknek az AB, BC, CA alaphoz tartozó magassága, és e 3 háromszög együttes területe egyenlő az ABC háromszög t területével:
AB⋅ϱ2+BC⋅ϱ2+CA⋅ϱ2=ϱ2(AB+BC+CA)=AB⋅CD2,
amiből DO=ϱ=615. ϱ'-t hasonlóan kapjuk: a BCH és CAH háromszögek területének összegéből az ABH háromszög területét kivonva ismét ABC területét kapjuk:
BC⋅ϱ'2+CA⋅ϱ'2-AB⋅ϱ'2=BC⋅CD2,DH=ϱ'=AB⋅CDBC+CA-AB=1015.


Most már a kérdéses távolságokat DS, DM, DK, D0, DH-ból kivonással és összeadással abból kapjuk, hogy mindegyik vizsgálandó pont és D is az ABC▵ tengelyén van, éspedig H kivételével mindegyik a háromszög belsejében (ugyanis a háromszög hegyesszögű, mert alapja kisebb a száránál, ezért M és K belső pontok). Így
KS=SO=OM=415,KO=SM=815,KM=MH=1215,OH=1615,SH=2015,KH=2415,


vagyis ebben a speciális háromszögben a K, S, 0, M pontok egymástól egyenlő távolságban sorakoznak a tengelyen és M-től C' is ennyire van, mert DC'=2r-m=215.
 
 Somos Péter (Budapest, Rákóczi F. g. II. o. t.)
 
Megjegyzés. Többen kimondták, hogy a vizsgált háromszögben csak O (és H) elhelyezkedése a különösség, ‐ hogy ti. O felezi az SM szakaszt. Bebizonyítható ugyanis, hogy M, S, K minden nem egyenlő oldalú háromszögben is egy egyenesen (a háromszög ún. ,,Euler‐féle egyenesén'') fekszik ‐ így pedig az SCM és SDK háromszögek hasonlóságából és az SC:SD=2:1 arányból adódik, hogy SM=2SK.)