Feladat: 738. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Berendi Emma ,  Csada Imre ,  Régi Erzsébet 
Füzet: 1962/november, 134 - 136. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1961/december: 738. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. A szögek egyszerű aránya alapján az ábrát többféleképpen is kiegészíthetjük úgy, hogy tartalmazzon egyenlő szárú háromszöget. Az I. megoldás az elemzéshez a legkevesebb és a legtermészetesebb kiegészítést veszi, tovább viszont a többieknél erősebb eszközöket használ.

 
I. megoldás. Képzeljük a feladatot megoldottnak és legyen a keresett ABC háromszögben BC=a=4 cm, AC=b=5 cm és β=ABC∢=2BAC∢=2α. Messe az ABC szög felezője AC-t D-ben. Az ABD háromszög A-nál és B-nél levő szögei egyenlők, ezért BD=AD, másrészt BDC∢=2BAD∢=ABC∢, tehát a BDC háromszög hasonló ABC-höz, mert szögeik egyenlők. Így
CD:CB=CB:CA,(1)
vagyis CB mértani középarányos CA és az ismeretlen CD között, tehát CD megszerkeszthető. Ebből megkapjuk DB=DA-t, ennélfogva a CDB háromszög is megszerkeszthető.
 
 
1. ábra
 

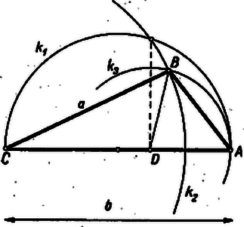Egy lehetőség a végrehajtásra: az adott AC szakasz mint átmérő fölé k1 (Thalész-) kört és C körül az adott CB sugárral k2 kört írunk, metszéspontjuknak AC-n levő vetülete D; a D körül DA sugárral írt k3 kör k2-ből kimetszi B-t, a keresett háromszög harmadik csúcsát.
A nyert ABC háromszögben AC, CB hossza az előírás szerinti, másrészt DA=DB miatt BDC∢=2BAC∢; (1) alapján a közös szögű ABC és BDC háromszögek hasonlók, így ABC∢=BDC∢=2BAC∢, tehát ABC háromszög megfelel a követelményeknek. Két B pontot kapunk, de ezek AC-re tükrösek, csak egy megoldás van.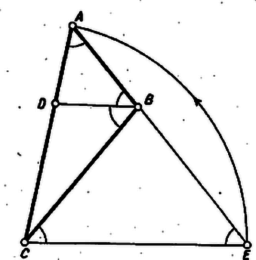
 
 Régi Erzsébet (Székesfehérvár, Teleki B. lg. II. o. t.)
 
Megjegyzés. Többen diszkussziót fűztek megoldásukhoz. Ennek itt nincs helye, mert AC és BC értéke rögzített, nincs változási lehetőség. Ilyenkor vagy van megoldás ‐ mint itt is ‐, vagy nincs.
 
 
2. ábra
 

II. megoldás. Messe a C-n át BD-vel párhuzamosan húzott egyenes AB meghosszabbítását E-ben (2. ábra). Ekkor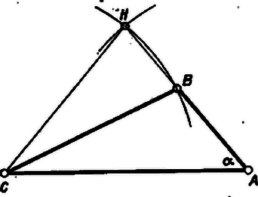
AEC∢=ABD∢=BAD∢=DBC∢=ECB∢,
részben a szerkesztés, részben a feladatnak a szögekre vonatkozó feltétele következtében. Így egyrészt az ACE, másrészt a CBE háromszög egyenlő szárú: EC=AC, EB=BC. A CBE háromszög mindegyik oldala ismert, tehát a háromszög 2BC>CE folytán megszerkeszthető. Ezután A-t mint a C körül CE sugárral rajzolt kör és az EB egyenes második metszéspontját kapjuk. CB<CE folytán ez E-től különböző pont, és B az A és E közt fekszik.
 
Az ABC háromszögben AC és BC a kívánt hosszúságú, másrészt BCE∢=CEB∢=CAE∢ és ABC∢=BCE∢+BEC∢=2CAE∢=2CAB∢. Így a nyert háromszög megfelel a feladat követelményeinek.
 
 Berendi Emma (Budapest, Ságvári E. gyak. lg. II. o. t.)
 
 
3. ábra
 

III. megoldás. Messe az AB egyenest a C körül BC sugárral rajzolt kör másodszor a H pontban (3. ábra). B és H különbözők, kivéve ha ABC∢=90∘, BAC∢=45∘, amikor BC=AC/2, de ez esetünkben nem áll fenn. A H pont vagy A és B közt van (BC<AC folytán), vagy AB-nek a B-n túli meghosszabbításán. Vizsgáljuk az AHC háromszöget. Az első esetben1 AHC∢=180∘-BHC∢=180∘-HBC∢=80∘-2α; a második esetben AHC∢=HBC∢=180∘-ABC∢=180∘-2α, így mindkét esetben ACH∢=180∘-α-(180∘-2α)=α, tehát az AHC háromszög egyenlő szárú, AH=HC=BC. Ennélfogva a keresett háromszög B csúcsát az AC=b alap fölé a szárral szerkesztett ACH egyenlő szárú háromszög AH szárából a C körül a sugárral írt körív metszi ki. ‐ A végrehajtás szempontjából ez a szerkesztés a legegyszerűbb, hiszen az említett körívet már az ACH háromszög szerkesztése közben megrajzoltuk.
 
 Csada Imre (Budapest, Petőfi S. g. II. o. t.)
1A méretekből az adódik, hogy itt a 2. esettel állunk szemben, ezt mutatja a 3. ábra. Ezen az 1. esetre elgondolt viszonyokat B és H felcserélésével szemlélhetjük.