Kezdőlap


Feladat:	737. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bock György , Gondol Ibolya
Füzet:	1962/október, 61 - 63. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Terület, felszín, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/december: 737. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C D$ trapézban $A B = 3 m$ , $C D = 2 m$ . Így a párhuzamos $C$ és $D$ egyikéből indul ki, legyen $D E ∥ C B$ . A trapéz és a $B C D E$ paralelogramma közös $B D$ átlójának $A C$ , $E C$ -vel való metszéspontját $K$ , ill. $L$ -lel jelölve a kérdéses $C K L$ háromszög $t$ területét a $C D L$ és $C D K$ háromszögek $t_{1}$ , $t_{2}$ területéből kivonással kaphatjuk. Az előbbi a paralelogramma 1/4 része, így 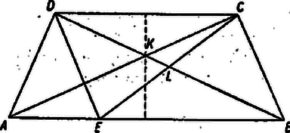$t_{1} = 2 m \cdot m / 4 = m^{2} / 2$ .

1. ábra

C D K

háromszög hasonló

A B K

-hoz, így

K

-ból húzott magasságaik aránya megegyezik az alapok

2 : 3

arányával, összegük viszont

m

, tehát

C D K

magassága

2 m / 5

, területe

t_{2} = 2 m^{2} / 5

. Ezek szerint

t = m^{2} / 10

. ‐ A trapéz területe viszont

T = 5 m^{2} / 2

, tehát valóban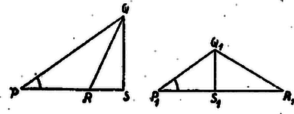

T / t = 25

Gondol Ibolya (Tapolca, Bacsányi J. g. I. o. t.)

Megjegyzés. Egy más felbontás (az idomok jele egyszersmind a területet is jelöli):

\begin{matrix} C K L = A B C - A B K - B C L = \frac{1}{2} (A E C - A E K) . \end{matrix}

2. ábra

II. megoldás. A

C K L △

területének kiszámításához a fenti hasonlóságból felhasználjuk, hogy

C K : A K = 2 : 3

, és így

C K = 2 C A / 5

. Másrészt

C L = C E / 2

. A

C K L

és

C A E

háromszögek

C

-nél levő szöge közös, ezért területeik aránya ‐ mint alább megmutatjuk ‐ megegyezik a

C

-ből kiinduló oldalaikból képezett szorzatok arányával:

\begin{matrix} C K L : C A E = (C K \cdot C L) : (C A \cdot C E) = (\frac{2}{5} C A \cdot \frac{1}{2} C E) : (C A \cdot C E) = 1 : 5. \end{matrix}

Ámde a

C A E

háromszög területe

m^{2} / 2

, mert

A E = A B - D C = m

, tehát ismét

C K L = m^{2} / 10

.
A felhasznált segédtétel bebizonyítása végett húzzuk meg a

P Q R

és

P_{1} Q_{1} R_{1}

háromszögekben ‐ amelyekben

Q P R ∢ = Q_{1} P_{1} R_{1} ∢

‐, a

Q S

Q_{1} S_{1}

magasságot. Ekkor a

P Q S

és

P_{1} Q_{1} S_{1}

derékszögű háromszögek hasonlóságát felhasználva

\begin{matrix} P Q R : P_{1} Q_{1} R_{1} = \frac{P R \cdot Q S}{2} : \frac{P_{1} R_{1} \cdot Q_{1} S_{1}}{2} = \\ = P R \frac{Q S}{Q_{1} S_{1}} : P_{1} R_{1} = P R \frac{Q P}{Q_{1} P_{1}} : P_{1} R_{1} = \frac{P R \cdot P Q}{P_{1} R_{1} \cdot P_{1} Q_{1}} . \end{matrix}

A segédtétel nyilván akkor is érvényes, ha

Q P R ∢ + Q_{1} P_{1} R_{1} = 180^{\circ}

Bock György (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

III. megoldás. Tetszés szerinti

A B C D

trapézban legyen

C D A ∢ > B C D ∢

. Bontsuk a trapézt a

B C

szárral párhuzamos

E D

szakasszal paralelogrammára és háromszögre. Messe a

B D

átlót

A C

, ill.

C E

K

, ill.

L

pontban. Meg fogjuk határozni a trapéz

T

területének és a

C K L

háromszög

t

területének az arányát. Legyenek a trapéz párhuzamos oldalai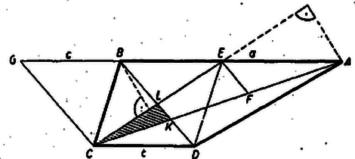

A B = a

C D = c

3. ábra

A trapézt az

A C D

A E C

és

B C E

háromszögekre bontottuk. Ezek közül az első és az utolsó egyenlő területű, mert

B E = C D = c

(egy paralelogramma szemben fekvő oldalai), és az ehhez tartozó magasságok is egyenlők (a trapéz magassága). Jelöljük ezt a területet

t'

-vel, az

A E C

háromszög területet

t''

-vel. Ezek aránya, mint pl. a

C E

oldal mentén csatlakozó két háromszög területének aránya, megegyezik a közös oldalhoz tartozó magasságok arányával, az pedig a

B E / A E

aránnyal:

\begin{matrix} \frac{t'}{t''} = \frac{B E}{A E} = \frac{c}{a - c}; T = 2 t' + t'' = (\frac{2 c}{a - c} + 1) t'' = \frac{a + c}{a - c} t'' . \end{matrix}

A keresett arány meghatározásához a

t'' / t

arányra van még szükségünk. Húzzunk

E

-ből

B D

-vel párhuzamos

E F

szakaszt a

C A

egyenesig. Ekkor, mivel

C E = 2 C L

B C D E

paralelogramma átlói felezik egymást), így a

C K L

háromszöghöz hasonló

C E F

háromszög területe

4 t

. A

t'' / 4 t

arányt úgy határozhatjuk meg, mint az

A E C

és

C E F

háromszögek területének az arányát. Ez megegyezik a közös magassággal rendelkező

A C

és

F C

oldalak arányával. Húzzunk

C

-ből párhuzamost

B D

-vel, messe ez

A B

meghosszabbítását

G

-ben. Ekkor

B G = c

, s így

\begin{matrix} \frac{t''}{4 t} = \frac{A C}{F C} = \frac{A G}{E G} = \frac{a + c}{2 c}, t'' = 2 \frac{a + c}{c} t . \\ T = \frac{a + c}{a - c} t'' = 2 \frac{{(a + c)}^{2}}{c (a - c)} t . \end{matrix}

T / t

arányt

a

és

c

, sőt már arányuk:

a / c

is meghatározza:

\begin{matrix} T = 2 \frac{{(a + 1)}^{2}}{a - 1} t . \end{matrix}

A feladatban

a = 3 / 2

, s így

\begin{matrix} T = 2 \frac{{(5 / 2)}^{2}}{1 / 2} t = 25 t . \end{matrix}

A feladatban fölösleges adat tehát a párhuzamos oldalak viszonya a magassághoz, csak az arányukra volt szükségünk. Azt sem használtuk ki (egyik bizonyításban sem), hogy a trapéz szimmetrikus.