Kezdőlap


Feladat:	732. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Komlós György , Máté Attila , Nagy László
Füzet:	1962/október, 54 - 56. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Vektorok skaláris szorzata, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/november: 732. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. $A C > B D$ miatt a paralelogrammának $A$ -nál levő szöge és $B$ , $D$ -nél levő külső szöge hegyes szög, ezért $E$ az $A B$ oldal $B$ -n túli, $F$ az $A D$ oldal $D$ -n túli meghosszabbítására esik.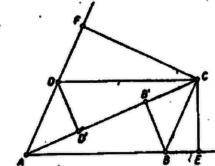

\begin{matrix} 1. ábra \end{matrix}

A C E

és

B C E

derékszögű háromszögekből

\begin{matrix} A C^{2} = A E^{2} + E C^{2} = A E^{2} + B C^{2} - B E^{2} = A E^{2} + B C^{2} - {(A E - A B)}^{2}, \\ A C^{2} = B C^{2} + 2 A B \cdot A E - A B^{2} . & (2) \end{matrix}

Hasonlóan az

A C F

és

D C F

derékszögű háromszögekből,

D F = A F - A D

behelyettesítésével

\begin{matrix} A C^{2} = D C^{2} + 2 A D \cdot A F - A D^{2} . \end{matrix}

(3)

Most már (2) és (3)-ból összeadással,

B C = A D

és

D C = A B

figyelembevételével, végül 2-vel osztva (1)-et kapjuk.

A C = B D

esetén a paralelogramma derékszögű,

E \equiv B

és

F \equiv D

, így (1) a Pythagorász tételre egyszerűsödik.

A C < B D

esetén az

A B C

szög hegyesszög. Feltehetjük, hogy

A B

-vel a paralelogramma nem kisebb oldalát jelöltük:

A B \geq B C

. Másrészt

B E < B C

, így

B E < A B

, tehát

E

A B

szakaszon van. Ezért (2) itt is érvényes, mert

B E

felhasznált kifejezése helyére a (

- 1

)-szerese lép, evvel azonban a négyzete nem változik meg.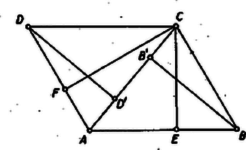

\begin{matrix} 2. ábra \end{matrix}

Ugyanez áll (3)-ra is abban az esetben, ha

F

A D

szakaszra, esetleg éppen

A

-ba esik (2. ábra), ilyenkor tehát (1) érvényes. Az

F \equiv A

esetben az

A B C

háromszög

C

-nél derékszögű és (1) az ismert mértani középarányos tételre egyszerűsödik: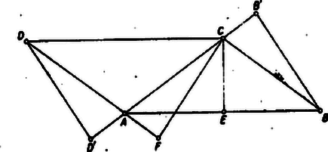

A C^{2} = A B \cdot A E

\begin{matrix} 3. ábra \end{matrix}

F

A D

oldal

A

-n túli meghosszabbítására esik, akkor

D F = A F + A D

(3. ábra). Ezt

D F = - (- A F - A D)

alakban írva (3) helyére a fenti módon

\begin{matrix} A C^{2} = D C^{2} - 2 A D \cdot A F - A D^{2}, \end{matrix}

(3')

és folytatólag (1) helyére a következő lép:

\begin{matrix} A B \cdot A E - A D \cdot A F = A C \cdot A C \end{matrix}

(1')

(1)-et és (

1'

)-t összefoglalva, egyszersmind a paralelogramma oldalaira tett megszorítást is feloldva (1)-et minden esetre érvényesnek mondhatjuk ki azzal a hozzáadással, hagy az

A B

A D

irányokat pozitívnak véve az

A E

A F

szakaszokat pozitív vagy negatív előjellel vesszük aszerint, hogy

A

-tól különböző végpontjuk

A

-nak a

B

-vel, ill.

D

-vel megegyező vagy ellentétes oldalán van.

Komlós György (Debrecen, Mechwart A. gépip. t. II. o. t.)

II. megoldás. Legyen

B

és

D

-nek

A C

-re való vetülete

B'

, ill.

D'

. A közös hegyes szöggel bíró

A C E

és

A B B'

derékszögű háromszögek hasonlók, ezért

\begin{matrix} A E : A B' = A C : A B, amiből (4) A B' = \frac{A B \cdot A E}{A C} . \end{matrix}

Ugyanígy az

A C F

és

A D D'

háromszögek hasonlók, továbbá az

A D D'

és

C B B'

háromszögek egybevágók, tehát

A C F

és

C B B'

hasonlók. Ebből

\begin{matrix} A F : C B' = A C : C B és (5) C B' = \frac{C B \cdot A F}{A C} = \frac{A D \cdot A F}{A C} . \end{matrix}

A B C

szög tompaszög, ezért

B'

A C

szakaszon van. Így (4) és (5) összeadásával

\begin{matrix} A B' + B' C = A C = \frac{A B \cdot A E + A D \cdot A F}{A C}, \end{matrix}

ebből pedig

A C

-vel átszorozva (1)-et kapjuk.
Az

A C < B D

(és

A B \geq B C

) esetre meg kell vizsgálnunk a paralelogramma középpontjára nyilvánvalóan tükrös

B'

D'

pontpár helyzetét. Aszerint amint

F

A D

szakaszra, vagy ennek meghosszabbítására esik, a

C A D

szög hegyes-, ill. tompaszög, ezért

D'

A C

szakaszon, ill. ennek

A

-n túli meghosszabbításán van. Csak az utóbbi helyzettel kell foglalkoznunk. Ekkor

A C = A B' - C B'

, és ismét (1)-re jutunk.

Nagy László (Budapest, I. István g. II. o. t.)

Megjegyzés. Az állítás a vektoralgebra módszerével is bizonyítható.

Máté Attila (Szeged, Radnóti M. g. I. o. t.)