Kezdőlap


Feladat:	730. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gáspár Sándor , Horváth Péter , Szörényi Miklós
Füzet:	1962/szeptember, 18 - 19. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/november: 730. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a szabályos háromszög $A B C$ , vegyük első, második, harmadik oldalnak rendre $B C$ -t, $C A$ -t, $A B$ -t, és legyen a $B C$ szakasz felezőpontja $D$ . A szimmetria miatt elég az állítást a $D$ kezdőpontú, $B$ -n átmenő félegyenesen vett $P$ kiindulópontokra igazolnunk. Legyen a két merőleges talppontja $P_{2}$ , $P_{3}$ , a párhuzamos metszéspontja $Q$ , ekkor azt kell bebizonyítani, hogy 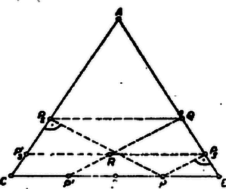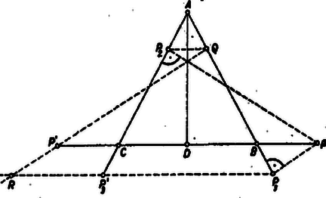$P_{3} Q = D P$ .
Ha $P$ a $D$ -ben vagy a $B$ -ben van, az állítás nyilvánvalóan igaz, mert az első esetben $P_{2}$ és $P_{3}$ tükrösek az $A D$ tengelyre és így $Q \equiv P_{3}$ , a másodikban pedig $P_{3} \equiv B$ , $P_{2}$ és $Q$ oldalfelező pontok, és így mindkét szakasz $B C / 2$ -vel egyenlő.
Ha $P$ a $D B$ szakasz pontja, akkor $P_{2}$ a $C A$ szakaszon, $Q$ és $P_{3}$ a $B A$ szakaszon van. A $P B P_{3}$ és $P C P_{2}$ derékszögű háromszögek hasonlók $A B D$ -höz, ezért $B P_{3} = B P / 2$ , $C P_{2} = C P / 2$ , továbbá a szimmetria miatt $B Q = C P_{2}$ . Mivel $B P < C P$ , és így $B P_{3} < C P_{2}$ , azért (1. ábra)

\begin{matrix} P_{3} Q = B Q - B P_{3} = C P_{2} - B P_{3} = \\ = \frac{C P - B P}{2} = \frac{(C D + D P) - (B D - D P)}{2} = D P, \end{matrix}

ugyanis

C D = B D

1. ábra

2. ábra

P

átlép

C B

-nek

B

-n túli meghosszabbítására, akkor

P_{2}

C A

Q

pedig a

B A

félegyenesen adódik,

P_{3}

pedig

A B

-nek

B

-n túli meghosszabbításán. Az előbbiekhez részben hasonlóan (2. ábra)

\begin{matrix} P_{3} Q = P_{3} B + B Q = P_{3} B + C P_{2} = \\ = \frac{B P + C P}{2} = \frac{(D P - D B) + (C D + D P)}{2} = D P . \end{matrix}

Eszerint az állítást minden figyelembe veendő esetben helyesnek találtuk.

Horváth Péter (Budapest, Kossuth L. gépip. t. II. o. t.)

II. megoldás.

P

-nek csak a

B

és

D

-től különböző helyzeteivel foglalkozunk. Ábránkat

A D

-re tükrözve

B

és

C

, valamint

P_{2}

és

Q

egymásba mennek át, legyen

P

és

P_{3}

tükörképe (

D C

-n ill.

C P_{2}

-n)

P'

P'_{3}

, továbbá

P' Q

és

P_{3} P'_{3}

metszéspontja

R

. Ekkor

P' Q ⊥ A B

, mint az

A C

-re merőleges

P P_{2}

szakasz tükörképe, ezért

P' Q

párhuzamos

P P_{3}

-mal. Így a

P P_{3} R P'

négyszög paralelogramma (mert

P_{3} R ∥ B C

és

P_{3} R = P P' = 2 D P

). Másrészt az

R P_{3} Q

háromszög hasonló

A B D

-hez, te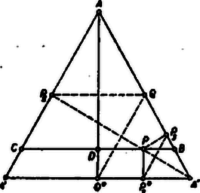hát

P_{3} Q = P_{3} R / 2 = D P

Gáspár Sándor (Budapest, I. István g. II. o. t.)

3. ábra

III. megoldás. Legyen

A

-nak

P_{2}

-re és

Q

-ra való tükörképe

A'

, ill.

A''

. Így

P_{2}

és

Q

A A' A''

háromszög oldalfelező pontjai, és

P_{2} A''

átmegy

P

-n, mert

P P_{2} ⊥ A A'

. Legyen

Q

és

P_{3}

tükörképe

A'' P_{2}

-re

Q^{*}

P_{3}^{*}

(3. ábra). Ekkor

Q^{*}

felezi

A' A''

-t, tehát rajta van az

A B C

és

A A'' A'

szabályos háromszögek közös

A D

tengelyén, ezért

D Q^{*} ⊥ B C

. Továbbá

P P_{3}^{*} ⊥ A' A'' ∥ B C

, mert

P P_{3}^{*}

A B

-re merőleges

P P_{3}

tükörképe. Ezek szerint a

P D Q^{*} P_{3}^{*}

négyszög téglalap, tehát

P_{3} Q = P^{*} Q^{*} = P D

Szörényi Miklós (Pécs, Széchenyi I. g. I. o. t.)