Kezdőlap


Feladat:	725. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Földes Antónia , Gerencsér László , Kultsár Levente , Szentai Judit
Füzet:	1962/május, 215 - 218. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/október: 725. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk meg, hol fekszenek azok a $P$ pontok, amelyekre pl. $P_{1} P / P Q_{1}$ éppen $2$ , annál kisebb, ill. annál nagyobb. Legyen a $P_{1} P_{2} P_{3} = H$ háromszög $P_{2} P_{3}$ oldalának a felezőpontja $R_{1}$ . A $P_{1} R_{1}$ súlyvonalon az $S$ súlypontra lesz, mint ismeretes, a kivánt arány $2$ . Húzzunk $S$ -en át párhuzamost $H$ -nak $P_{2} P_{3}$ oldalával. Legyen ennek a $P_{1} P_{2}$ , ill. $P_{1} P_{3}$ oldalon levő metszéspontja $K_{3}$ , ill. $K_{2}$ , és egy tetszés szerinti $P_{1} Q_{1}$ szakasznak a közös pontja $K_{2} K_{3}$ -mal $K$ . Ha $P$ egybeesik $K$ -val, akkor 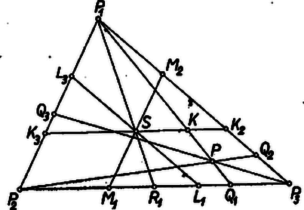$P_{1} P / P Q_{1} = P_{1} S / S R_{1} = 2$ . Ha $P$ a $P_{1} K$ szakaszon van, akkor

\begin{matrix} \frac{P_{1} P}{P Q_{1}} < \frac{P_{1} K}{K Q_{1}} = 2, \end{matrix}

mert az első tört számlálója helyére nagyobb, nevezője helyére kisebb szakaszt írtunk. Végül ha

P

K Q_{1}

szakaszon van, akkor hasonló meggondolással

\begin{matrix} \frac{P_{1} P}{P Q_{1}} > \frac{P_{1} K}{K Q_{1}} = 2, \end{matrix}

mert, így

P_{1} P > P_{1} K

és

P Q_{1} < K Q_{1}

1. ábra

Megállapításainkat így is kimondhatjuk: A

P_{1} P / P Q_{1}

hányados értéke kisebb ill. nagyobb

2

-nél aszerint , hogy

P

P_{1} K_{2} K_{3} = H_{1}

háromszög belsejében, ill. a

P_{2} P_{3} K_{2} K_{3} = T_{1}

trapéz belsejében van, és a hányados értéke

2

, ha

P

H_{1}

és

T_{1}

közös

K_{2} K_{3}

határszakaszának pontja.

H

-t az

S

-en átmenő,

P_{3} P_{1}

-gyel párhuzamos

L_{3} L_{1}

szakasszal

P_{2} L_{3} L_{1} = H_{2}

és

P_{3} P_{1} L_{3} L_{1} = T_{2}

trapézra osztva hasonlóan kapjuk, hagy a

P_{2} P / P Q_{2}

hányados értéke a

H_{2}

-beli

P

pontokra kisebb, a

T_{2}

-beliekre nagyobb

2

-nél és az

L_{3} L_{1}

szakaszon levő pontokra egyenlő

2

-vel, továbbá hogy a

P_{1} P / P Q_{3}

hányados a

P_{3} M_{1} M_{2} = H_{3}

háromszög pontjaira kisebb, a

P_{1} P_{2} M_{1} M_{2} = T_{3}

trapéz pontjaira nagyobb

2

-nél, és az

M_{1} M_{2}

szakaszon vett

P

-re egyenlő

2

-vel, ha

M_{1} M_{2}

átmegy

S

-en és párhuzamos

P_{1} P_{2}

-vel. Ezek alapján az állítás bizonyítására elég azt belátnunk, hogy

H

belsejében nincs olyan

P

pont, amely

H

-nak

K_{2} K_{3}

L_{3} L_{1}

és

M_{1} M_{2}

-vel való kettévágásai során mindhárom esetben a trapéz belsejébe esnék, és olyan

P

sincs, amely mindháromszor a megfelelő

H_{1}

H_{2}

, ill.

H_{3}

-háromszög belsejébe esnék.
Valóban, a

T_{1}

és

T_{2}

trapézok közös részének, a

P_{3} K_{2} S L_{1}

paralelogrammának belseje a

H_{3}

háromszög belsejébe esik, tehát nincs közös pontja

T_{3}

-mal, és hasonlóan

H_{1}

és

H_{2}

közös részének, a

K_{3} S L_{3}

háromszögnek belseje

T_{3}

belsejébe esik, nincs közös pontja

H_{3}

-mal. Ezzel az állítást bebizonyítottuk.
A bizonyításból az is következik, hogy ha

P

nem azonos a

H

háromszög súlypontjával, akkor a vizsgált arányok között van

2

-nél nagyobb értékű is,

2

-nél kisebb értékű is, mert

S

-et kivéve minden pont csak egy kettévágó szakaszhoz tartozik hozzá.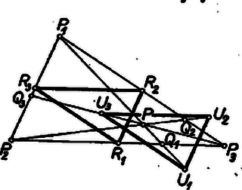

Kultsár Levente (Hajdúböszörmény, Bocskai I. g. II. o. t.)

II. megoldás. Az, hogy

P_{1} P / P Q_{1}

2

-nél kisebb, vele egyenlő, vagy nagyobb nála, úgy is fogalmazható, hogy

P_{1} P / 2

kisebb

P Q_{1}

-nél, egyenlő vele, vagy nagyobb nála. Így

P_{1} P

-t meghosszabbitva a

P

ponton túl a másfélszeresére, a keletkező

U_{1}

végpont a

P Q_{1}

szakasz, és így egyben a háromszög belsejében van, ill. egybeesik

Q_{1}

-gyel, ill.

Q_{1}

-en túl, tehát a háromszögön kívül van, amint

P_{1} P / P Q_{1}

kisebb

2

-nél, egyenlő vele, vagy nagyobb, mint

2

. Hasonló érvényes a

P_{2} P

és

P_{3} P

szakasz

P

-n túl másfélszeresére nyújtásával keletkező

U_{2}

U_{3}

végpontokra.

2. ábra

A feladat állítása ennek segítségével a következő módon fogalmazható át: az

U_{1}

U_{2}

U_{3}

pontok nem lehetnek mind a

H

háromszögön kívül, sem nem lehetnek mind a háromszög belsejében. Ezt fogjuk bebizonyítani.
Az

U_{1} U_{2} U_{3} = H_{u}

háromszög

H

-ból előállítható

P

körül való

180^{\circ}

-os forgatással és

1 : 2

arányú egyidejű kicsinyítéssel. Ugyanez áll az oldalfelező pontok alkotta

R_{1} R_{2} R_{3} = H_{r}

háromszögre, forgatási középpontnak az

S

súlypontot véve. Eszerint

H_{u}

és

H_{r}

egybevágók, megegyező állásúak, egymásba eltolással átvihetők. Erre támaszkodva megmutatjuk, hogy ha

U_{1}

és

U_{2}

egyike sem belső pont, akkor

U_{3}

belső pont. Ugyanis

U_{1} U_{2} \neq R_{1} R_{2}

, ill.

U_{1} U_{2}

nem párhuzamos

R_{1} R_{2}

; és ez csak úgy lehet, hogy

U_{1} U_{2}

R_{1} R_{2}

-nek azon a partján van, mint

P_{3}

, mert

U_{1}

és

U_{2}

P_{1} P_{2}

egyenesnek azon a partján van, mint

R_{1}

R_{2}

, így ha

R_{1} R_{2}

-nek ellenkező partján lenne

U_{1}

U_{2}

, mint

P_{3}

, akkor az

U_{1} U_{2}

egyenesnek

R_{1} R_{2}

-nél hosszabb szakasza esnék

H

-ba, és így

U_{1}

és

U_{2}

közül legalább az egyik

H

belsejében volna. Így

H_{u}

-val együtt

U_{3}

P_{1} P_{2}

-nek

P_{3}

-mal egyező partjára jut. Viszont szerkesztésénél fogva

U_{3}

P_{2} P_{3}

-nak

P_{1}

-gyel egyező partján és

P_{1} P_{3}

-nak

P_{2}

-vel egyező partján van, tehát benne van

H

-ban.
Hasonlóan bizonyítható, hogy ha

U_{1}

és

U_{2}

egyike sem külső pont, akkor

U_{3}

P_{1} P_{2}

ellenkező partjára esik, mint

P_{3}

, s így

H

-n kívül van.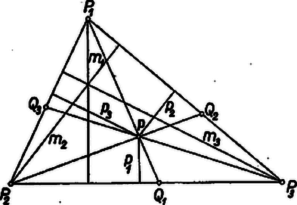

Földes Antónia (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

3. ábra

III. megoldás. Húzzunk merőlegest

P

-ből a

P_{2} P_{3}

P_{3} P_{1}

P_{1} P_{2}

oldalra, hosszuk legyen

p_{1}

p_{2}

p_{3}

, továbbá

H

megfelelő magasságai

m_{1}

m_{2}

m_{3}

. A keletkezett hasonló derékszögű háromszögek felhasználásával

\begin{matrix} \frac{P_{i} P}{P Q_{i}} = \frac{P_{i} Q_{i} - P Q_{i}}{P Q_{i}} = \frac{P_{i} Q_{i}}{P Q_{i}} - 1 = \\ = \frac{m_{i}}{p_{i}} - 1, \end{matrix}

ahol

i

1

2

3

indexek bármelyikét jelentheti. Eszerint elegendő megmutatnunk, hogy az

m_{i} / p_{i}

arányok között van olyan, amelyik nem nagyobb, mint

3

, és olyan is, amelyik nem kisebb

3

-nál.
A

P P_{2} P_{3}

P P_{3} P_{1}

és

P P_{1} P_{2}

háromszögek területének összege egyenlő

H

-nak

t

területével. Ebből átalakítással

\begin{matrix} t = \frac{P_{2} P_{3} \cdot p_{1}}{2} + \frac{P_{3} P_{1} \cdot p_{2}}{2} + \frac{P_{1} P_{2} \cdot p_{3}}{2} = \frac{P_{2} P_{3} \cdot m_{1}}{2} \cdot \frac{p_{1}}{m_{1}} + \\ + \frac{P_{3} P_{1} \cdot m_{2}}{2} \cdot \frac{p_{2}}{m_{2}} + \frac{P_{1} P_{2} \cdot m_{3}}{2} \cdot \frac{p_{3}}{m_{3}} = t (\frac{p_{1}}{m_{1}} + \frac{p_{2}}{m_{2}} + \frac{p_{3}}{m_{3}}) . \end{matrix}

Eszerint a

p_{i}

távolságokra és az

m_{i}

magasságokra fennáll:

\begin{matrix} \frac{p_{1}}{m_{1}} + \frac{p_{2}}{m_{2}} + \frac{p_{3}}{m_{3}} = 1. \end{matrix}

(1)

Jelöljük a

p_{1} / m_{1}

p_{2} / m_{2}

p_{3} / m_{3}

értékek közt előforduló legkisebb értéket

α

-val, az előforduló legnagyobbat

β

-val. Ekkor

\begin{matrix} 3 α ≦ \frac{p_{1}}{m_{1}} + \frac{p_{2}}{m_{2}} + \frac{p_{3}}{m_{3}} ≦ 3 β . \end{matrix}

Így (1)-ből következik, hogy

α ≦ 1 / 3

β ≧ 1 / 3

. Ezzel az állítást bebizonyítottuk.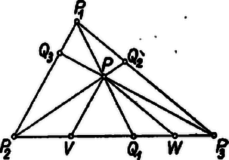

Szentai Judit (Budapest, Kanizsai Dorottya lg. I. o. t.)

4. ábra

IV. megoldás. Tegyük fel, hogy a

P_{2} P / P Q_{2}

és

P_{3} P / P Q_{3}

arányok értéke nem kisebb

2

-nél. Megmutatjuk, hogy ekkor

P_{1} P / P Q_{1}

nem nagyobb

2

-nél. Húzzunk

P

-n át párhuzamost

P_{1} P_{2}

-vel és

P_{1} P_{3}

-mal, és legyen ezeknek

P_{2} P_{3}

-mal való metszéspontja

V

, ill.

W

. A

P_{2} P W

P_{2} Q_{2} P_{3}

és a

P_{3} P V

P_{3} Q_{3} P_{2}

háromszög-párok hasonlósága és a feltevés alapján, mindjárt átalakítással

\begin{matrix} \frac{P_{2} P}{P Q_{2}} = \frac{P_{2} W}{W P_{3}} ≧ 2, \frac{P_{3} P}{P Q_{3}} = \frac{P_{3} V}{V P_{3}} ≧ 2. \end{matrix}

Az egyenlőtlenségek mindkét oldalához

1

-et adva

\begin{matrix} \frac{P_{2} W + W P_{3}}{W P_{3}} = \frac{P_{2} P_{3}}{W P_{3}} ≧ 3, \frac{P_{3} V + V P_{3}}{V P_{2}} = \frac{P_{2} P_{3}}{V P_{2}} ≧ 3, \end{matrix}

ezért

W P_{3} ≦ P_{2} P_{3} / 3

V P_{2} ≦ P_{2} P_{3} / 3

, és így

\begin{matrix} V W = P_{2} P_{3} - P_{3} W - P_{2} V ≧ P_{2} P_{3} - \frac{2 P_{2} P_{3}}{3} = \frac{1}{3} \cdot P_{2} P_{3} . \end{matrix}

(2)

Feltehetjük, hogy a betűzés olyan, hogy

V Q_{1} ≧ Q_{1} W

. Ekkor

V Q_{1} ≧ V W / 2 ≧ P_{2} P_{3} / 6

, és így

\begin{matrix} \frac{P_{1} P}{P Q_{1}} = \frac{P_{2} V}{V Q_{1}} ≦ \frac{\frac{P_{2} P_{3}}{3}}{\frac{P_{2} P_{3}}{6}} = 2. \end{matrix}

Ezt akartuk bizonyítani.
Hasonlóan nyerjük, hogy ha a vizsgálandó arányok közül kettőnek az értéke nem nagyobb

2

-nél, akkor a harmadiké nem kisebb

2

-nél.

Gerencsér László (Budapest, Rákóczi F. g. II. o. t.)