Feladat: 723. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Darabos Zsuzsanna 
Füzet: 1962/május, 214. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1961/október: 723. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az adott H háromszög A, B, C csúcsánál levő α, β, γ szög első harmadolóját rendre a', b', c'-vel, továbbá a' és b' metszéspontját C'-vel, b' és c'-ét A'-vel, c' és a' metszéspontját B'-vel. Ekkor az A'B'C'=H' háromszög A'-nél, B'-nél és C'-nél levő szöge, mint az A'BC, B'CA, C'AB háromszög külső szöge, így fejezhető ki: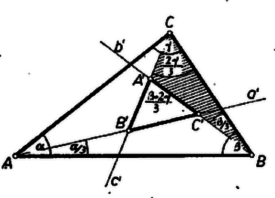

B'A'C'∢=α'=β+2γ3,C'A'B'∢=β'=γ+2α3,(1)A'C'B'∢=γ'=α+2β3.



 
 

Feltehetjük, hogy a betűzést úgy választottuk, hogy H-nak nincs sem α-nál kisebb, sem γ-nál nagyobb szöge, vagyis hogy
α≤β≤γ.

Így H' szögei között α'-nél nagyobb semmi esetre sincs, hiszen α'-ből β' is, γ' is csökkentéssel vagy változatlanul hagyással állítható elő:
α'=13(β+γ+γ)≥13(α+α+γ)=β',≥13(β+β+α)=γ'.
Eszerint, ha H és H' szögei páronkint megegyeznek, akkor
α'=γ,  azaz  β+2γ3=γ,  amiből  β=γ.
Így β' és γ' közül β' nem lehet a nagyobb, mert
γ'-β'=13(α+2β-γ-2α)=13(β-α),
ez pedig nem lehet negatív. Tehát
β'=α  és  γ'=β,
amiből (1) felhasználásával
γ+2α3=α,γ=α,ill.  α+2β3=β,α=β,
vagyis H szabályos háromszög. Így viszont (1) szerint α'=β'=γ', tehát H' is szabályos háromszög. Ezt kellett bizonyítanunk.
Darabos Zsuzsanna (Budapest, Apáczai Csere J. gyak. g. II. o. t.)
dolgozata alapján.

 
Megjegyzés. Számos versenyző tévesen azt bizonyította, hogy ha H szabályos, akkor H' is szabályos.