Feladat: 709. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ámon Magdolna ,  Corrádi G. ,  Csűrös M. ,  Deák I. ,  Dobó F. ,  Fazekas P. ,  Friss Ilona ,  Földeáki Mária ,  Földes Antónia ,  Földes I. ,  Gáspár Hedvig ,  Gazsó J. ,  Gerencsér L. ,  Geschek Péter ,  Gyárfás A. ,  Gönczy J. ,  Görbe T. ,  Harkányi G. ,  Horváth P. ,  Jahn L. ,  Kászonyi L. ,  Kiss G. ,  Klukovits l. ,  Koris K. ,  Kotsis D. ,  Krokos J. ,  Kultsár L. ,  Kultsár Sz. ,  Lajos Judit ,  Lehel Cs. ,  Lehel J. ,  Lipcsey Zs. ,  Major J. ,  Makai E. ,  Malatinszky G. ,  Markó J. ,  Mátrai M. ,  Mayer J. ,  Miklós A. ,  Müller Gy. ,  Nagy Angéla ,  Papp L. ,  Pásztor Gy. ,  Pázmándi L. ,  Raisz M. ,  Szekeres Veronika ,  Szép A. ,  Szepesvári Gy. ,  Szidarovszky F. ,  Tamás G. ,  Tasnády Mária ,  Vesztergombi F. 
Füzet: 1962/március, 117 - 119. oldal  PDF  |  MathML 
Témakör(ök): Magasságvonal, A háromszögek nevezetes pontjai, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1961/május: 709. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A 637. gyakorlat megoldása1 során említésre került, hogy ha az ABC=H háromszögben BAC∢=α>90∘, akkor ‐ M-mel a magasságpontot jelölve ‐ az MCB=H1 háromszög hegyesszögű és talpponti háromszöge ‐ a csúcsok sorrendjét tekintve is ‐ azonos H-nak A1B1C1=T talpponti háromszögével, továbbá H1 magasságpontja A (1. ábr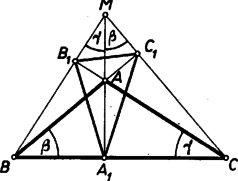a).

 
 
1. ábra
 

Valóban az MCB háromszögben
A1aCBegyenesenvan,MA1⊥CBésMA1átmegyA-n,B1aBM,,,,CB1≡CA⊥BMésCB1átmegyA-n,C1azMC,,,,BC1≡BA⊥MCésBC1átmegyA-n.

Hasonlóan bizonyítható, hogy a BAM=H2 és CMA=H3 háromszögek talpponti háromszöge ugyancsak T (sorrendre nézve is), magasságpontjaik pedig C, ill. B. ‐ Könnyű belátni, hogy ekkor H2 ben is, H3-ban is az A csúcsnál tompaszög van, továbbá azt is, hogy hegyesszögű H-ból kiindulva is H1, H2, H3 talpponti háromszöge mindig T, és magasságpontjuk rendre A, C, B (2. á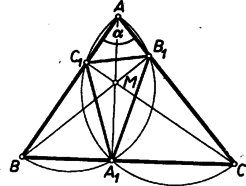bra).
 
 
2. ábra
 

Ezzel T-hez felsoroltunk 4 különböző olyan háromszöget, melyben a magasságtalppontok éppen T csúcsai. Megmutatjuk, hogy több ilyen háromszög nincs.
A 637. gyakorlat megoldásában azt is láttuk, hogy ha ABC és ACB hegyesszögek, akkor az A1A magasság A1B1-gyel és A1C1-gyel egyenlő szögeket zár be, és B1, C1 e magasság két oldalán vannak. Eszerint A1A felezi a B1A1C1 szöget. Hasonlóan látható be, hogy bármely nem derékszögű háromszög 3 magasságegyenese és 3 oldalegyenese felezi a talpponti háromszög egy belső vagy egy külső szögét, és így a talpponti háromszög mindegyik csúcsában a belső és külső szögfelezők egyike oldalegyenes, a másika pedig magasságegyenes.
Eszerint azon háromszögek oldalegyenesei, melyeknek talpponti háromszöge egy előre adott T háromszög, csak T belső és külső szögfelezői közül kerülhetnek ki. A mondott háromszögek csúcsai pedig csak a szögfelezők metszéspontjai közül valók lehetnek. ‐ Ámde a belső és külső szögfelezők bármely háromszögre nézve 3-asával 4 pontban, a 4 érintő kör (a beírt kör és a 3 hozzáírt kör) középpontjában metszik egymást, ezeken (és a háromszög csúcsain) kívül más közös pontjuk nincs. E 4 pont közül egy háromszög csúcsait valóban csak 4-féleképpen lehet választani (közülük sorra 1-et‐1-et elhagyva). Ezzel az állítást bebizonyítottuk.
 
b) A 637. gyakorlat megoldása szerint, ha a háromszög szögei α, β, γ és ezek mindegyike hegyesszög, akkor talpponti háromszögének szögei:
α'=180∘-2α,β'=180∘-2β,γ'=180∘-2γ;(1)
ha pedig α>90∘, akkor T szögei:
α'=2α-180∘,β'=2β,γ'=2γ.(2)

Adatainkat az (1) képletekkel csak egyféleképpen azonosíthatjuk, mert ez a 3 képlet azonos szerkezetű; a
180∘-2α=24∘,180∘-2β=60∘,180∘-2γ=96∘
egyenletrendszerből
I:α=78∘,β=60∘,γ=42∘.
A (2) képlethármassal való azonosítás viszont 3 féleképpen lehetséges aszerint, hogy a megkülönböztetett 2α-180∘ szerepet az adott szögek melyike kapja. A

2α-180∘=24∘,2β=60∘,2γ=96∘rendszerbőlII:α=102∘,β=30∘,γ=48∘,


és hasonlóan adódnak a

III:12∘,120∘,48∘ésIV:12∘,30∘,138∘

megoldások.
Annak belátására, hogy az I‐IV szöghármasok valóban egy-egy háromszög szögei, elég rámutatni, hogy (1) és (2)-ből α+β+γ értéke
270∘-α'+β'+γ'2ill.90∘+α'+β'+γ'2,
viszont az adott szögek összege α'+β'+γ'=180∘.
 
Geschek Péter (Budapest, József A. g. II. o. t.)
1K. M. L. 22 (1961) 110. o.