Kezdőlap


Feladat:	707. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ámon Magdolna , Baróti Gy. , Berecz Ágota , Corrádi G. , Csűrös M. , Deák I. , Dobó F. , Dudinszky Ilona , Fazekas P. , Fejéregyházi S. , Földeáki Mária , Földes Antónia , Gazsó J. , Gerencsér L. , Gyárfás A. , Gönczy J. , Görbe T. , Kászonyi L. , Kiss Gábor , Klukovits l. , Kotsis D. , Lehel Cs. , Lehel Jenő , Lőrincz Cs. , Lukács Lídia , Major J. , Malatinszky G. , Marosi Judit , Meskó L. , Mihályi Z. , Papp L. , Pusztai D. , Pusztai T. , Rejtő Lídia , Strobl Ilona , Szekeres Veronika , Szidarovszky F. , Szirai J.
Füzet:	1962/március, 115 - 116. oldal		PDF \| MathML
Témakör(ök):	Másodfokú diofantikus egyenletek, Derékszögű háromszögek geometriája, Hozzáírt körök, Pitagoraszi számhármasok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/május: 707. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az oldalak mértékszámai pythagorászi számhármast alkotnak, éspedig alaphármast, ennélfogva van olyan $m, n$ relatív prím, különböző párosságú pozitív egész számpár, $m > n$ , hogy az oldalak

\begin{matrix} a = m^{2} - n^{2}, b = 2 m n, c = m^{2} + n^{2}, \end{matrix}

(1)

ahol

c

az átfogó¹.

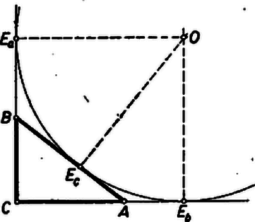Ismeretes másrészt, hogy minden derékszögű háromszögben az átfogóhoz hozzáírt kör

O E_{a} = O E_{b}

sugara egyenlő a kerület felével (a jelöléseket lásd az ábrán). Ugyanis a derékszög miatt

O, E_{a}

C

E_{b}

egy négyzet csúcsai, ezért a sugár egyenlő a derékszög szárain levő érintési pontoknak a derékszög csúcsától mért

C E_{b} = C E_{a}

távolságával. Ez a távolság viszont bármely háromszögben egyenlő a kerület felével, mert a körhöz egy külső pontból húzott érintőszakaszok egyenlők, ezért

\begin{matrix} C E_{b} + C E_{a} = C A + A E_{b} + C B + B E_{a} = C A + C B + (A E_{c} + B E_{c}) = \\ = b + a + c = 2 s, \end{matrix}

tehát

C E_{b} = s

.
Eszerint esetünkben

m

n

-nel kifejezve

\begin{matrix} ϱ_{c} = m^{2} + m n = m (m + n) = 420. \end{matrix}

(2)

Itt

m + n

biztosan páratlan, mint egy páros és egy páratlan szám összege, ezért

m

páros, sőt 4-gyel is osztható. Továbbá

m + n > m

, mert

n

pozitív, így

m

kisebb,

m + n

pedig nagyobb, mint 420 négyzetgyöke, ami

20, 4 ...

, azaz

m \leq 20

és

m + n \geq 21

. Másrészt

n < m

miatt

m + n < 2 m

, ezért (2)-ből

\begin{matrix} m \cdot 2 m = 2 m^{2} > 420, m > \sqrt[]{210} = 14, 4 ..., \end{matrix}

tehát

m \geq 16

.
Ezek szerint

m

értéke csak 16 vagy 20 lehet. Azonban 420 nem osztható 16-tal; a másik lehetőséggel viszont

\begin{matrix} m = 20, m + n = 21, n = 1, \end{matrix}

és így (1)-ből

a = 399

b = 40

c = 401

Lehel Jenő (Budapest, Apáczai Csere J. g. II. o. t.)

Megjegyzések. 1. Hasonló meggondolással célhoz érhetünk a pythagorászi alaphármasok

\begin{matrix} a = u v, b = \frac{u^{2} - v^{2}}{2}, c = \frac{u^{2} + v^{2}}{2} \end{matrix}

képletrendszeréből² is, ebben

u, v

relatív prímek, páratlanok, és

u > v

2. A megoldások legtöbbje hosszabb meggondolásokkal választotta ki a (2)-nek, ill. a jelzett második úton az ennek megfelelő egyenlőségnek eleget tevő egész számpárokból a megfelelőt.

¹Lásd K.M.L. (1961) 3. o. lábjegyzet

²Ugyanott