Kezdőlap


Feladat:	701. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baróti Gy. , Corrádi G. , Csűrös M. , Doskar B. , Fejéregyházi Sándor , Földes Antónia , Gerencsér L. , Gönczy J. , Harkányi G. , Koris K. , Kotsis D. , Kultsár Sz. , Lehel J. , Lőrincz Cs. , Lukács Lídia , Mészáros L. , Pusztai D. , Pusztai T. , Szidarovszky F. , Szirai J.
Füzet:	1962/január, 53 - 54. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/április: 701. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C = H$ háromszögre vonatkozóan megszerkesztett körök egyik közös pontja az $M$ magasságpont. A második metszéspontokat jelöljük $A_{2}$ , $B_{2}$ , $C_{2}$ -vel az ábrák szerint. Megmutatjuk, hogy $A_{2}$ , $B_{1}$ , $C_{1}$ , hasonlóan $B_{2}$ , $C_{1}$ , $A_{1}$ és $C_{2}$ , $A_{1}$ , $B_{1}$ egy egyenesre esnek, továbbá hogy $A_{2}$ , $B_{2}$ , $C_{2}$ az $M$ pont vetületei az $A_{1} B_{1} C_{1} = T$ talpponti háromszög oldalegyenesein. Elég ezt szimmetria-okokból pl. $A_{2}$ -re belátni. $M A_{2} B_{1} ∢ = M A_{2} C_{1} ∢ = 90^{\circ}$ , mert $A_{2}$ az $M B_{1}$ és $M C_{1}$ fölé rajzolt Thalész-körök metszéspontja; így $B_{1}$ és $C_{1}$ az $M A_{2}$ -re $A_{2}$ -ben emelt merőlegesen van, és ezt mondja állításunk.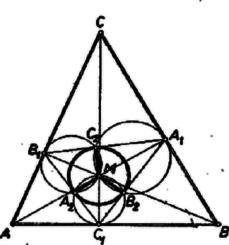

\begin{matrix} 1. ábra \end{matrix}

Így az

M A_{2}

M B_{2}

M C_{2}

húrok egyenlőségéhez azt kell belátnunk, hogy

M

egyenlő távolságra van

T

mindhárom oldalegyenesétől. Evégett bebizonyítjuk, hogy az

A_{1} M

B_{1} M

C_{1} M

magasságegyenesek ‐ ha

H

hegyesszögű ‐ felezik

T

-nek megfelelő belső szögét, tompaszögű

H

esetében pedig két külső és egy belső szögét.
Ha

H

hegyesszögű (1. ábra), akkor a magasság-talppontok az oldalszakaszokon vannak, és bármelyik két csúcs és a belőlük húzott magasságok talppontjai egy húrnégyszög csúcsai (egy oldal fölötti Thalész-körben). Az

A B A_{1} B_{1}

és

A C A_{1} C_{1}

húrnégyszögekből az

α

szög és a szemben fekvő szög külső szögének egyenlőségéből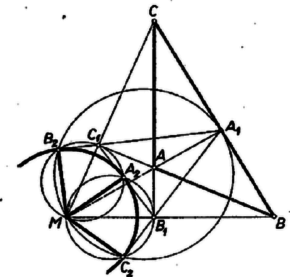

\begin{matrix} B_{1} A_{1} C ∢ = C A B ∢ = α = C_{1} A_{1} B ∢, \end{matrix}

és így az ezeket a szögeket

90^{\circ}

-ra kipótló

M A_{1} B_{1}

és

M A_{1} C_{1}

szögek is egyenlők, állításunknak megfelelően. Hasonló okoskodás érvényes a másik két magasságra is.

\begin{matrix} 2. ábra \end{matrix}

H

tompaszögű (

B A C ∢ > 90^{\circ}

, 2. ábra), akkor

B C M

hegyesszögű háromszög, magasságegyenesei az

A M

A B

A C

egyenesek, talpponti háromszöge szintén

T

. Így

A M

A_{1}

-nél levő belső szöget felezi;

B M

és

C M

viszont merőleges a

B_{1}

-nél, ill.

C_{1}

-nél levő belső szöget felező

A C

, ill.

A B

egyenesre, s így ezek

T

megfelelő külső szögeit felezik.
Ezzel a bizonyítást befejeztük. Megállapításunkat így is mondhatjuk:

M

T

-re nézve vagy a beírt, vagy az egyik hozzáírt kör középpontja, a vizsgált húrok pedig ezen körnek a

T

oldalain levő érintési pontokhoz tartozó sugarak.

Fejéregyházi Sándor (Budapest, I. István Gimn., II. o. t.)