Kezdőlap


Feladat:	693. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Doskar B. , Fazekas P. , Kászonyi L. , Kovács Gergely , Mészáros György , Mészáros L. , Szidarovszky F. , Tamás Géza , Tihanyi László
Füzet:	1962/január, 45 - 48. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/március: 693. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $a_{1}$ egyenes metszheti a háromszög $A B$ , $A C$ oldalait, azok $A$ -n túli meghosszabbításait, vagy a $B C$ oldalon túli meghosszabbításait. A három eshetőséget külön-külön vizsgáljuk.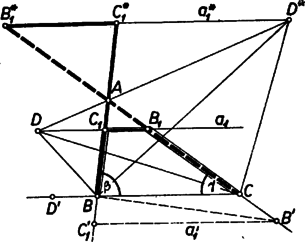

1. ábra

1. Tegyük fel, hogy

a_{1}

egy olyan megoldása a feladatnak, amelynél

B_{1}

C_{1}

A C

A B

oldalszakaszon van (1. ábra). Mérjük fel a

B C_{1}

szakaszt

C_{1} B_{1}

-nek

C_{1}

-en túli meghosszabbítására. A végpontot

D

-vel jelölve a

B C_{1} D

háromszög egyenlő szárú, ezért

\begin{matrix} D B C_{1} ∢ = \frac{1}{2} B C_{1} B_{1} ∢ = \frac{1}{2} (180^{\circ} - A B C ∢), \end{matrix}

tehát

B D

felezi az

A B C

háromszög

B

-nél levő külső szögét. Másrészt a

C B_{1} D

háromszög is egyenlő szárú, mert

D B_{1} = D C_{1} + C_{1} B_{1} = B C_{1} + C_{1} B_{1} = C B_{1}

. Ezért

\begin{matrix} D C B_{1} ∢ = \frac{1}{2} A B_{1} D ∢ = A C B ∢, \end{matrix}

tehát

C D

felezi az

A B C

háromszög

C

-nél levő szögét.
Ezek szerint

D

a mondott szögfelezők metszéspontja, és a keresett

a_{1}

D

-n átmenő,

a

-val párhuzamos egyenes.
Szerkesztésünk helyességének bizonyítására megmutatjuk, hogy az

a_{1}

és

A B

egyenesek

C_{1}

metszéspontja

A

és

B

között van. Ha ezt tudjuk, akkor a fönti meggondolás könnyen megfordítható a szerkesztés igazolására. Azt akarjuk belátni, hogy a

D

-n át

B C

-vel párhuzamosan húzott egyenes a

C

-t tartalmazó

A D B

szögtéren halad keresztül. Ez következik abból, ha megmutatjuk, hogy

A D B ∢ + D B C ∢ > 180^{\circ}

. A

D

pont az

A B C

háromszög

A B

oldalához hozzáírt külső érintőkör középpontja, ezért

A D

felezi az

A

csúcsnál levő külső szöget, tehát a szokásos jelölésekkel

D A B ∢ = (β + γ) / 2

. Így

\begin{matrix} A D B ∢ + D B C ∢ = (180^{\circ} - D A B ∢ - D B A ∢) + (D B A ∢ + A B C ∢) = \\ = 180^{\circ} - D A B ∢ + A B C ∢ = 180^{\circ} - \frac{β + γ}{2} + β = 180^{\circ} + \frac{β - γ}{2} . \end{matrix}

Ez nagyobb

180^{\circ}

-nál, mert feltétel szerint

A B < A C

, s így

γ < β

. Ebből következik, hogy

a_{1}

és

A C

-nek

B_{1}

metszéspontja

A

és

C

között van, továbbá, hogy

C_{1}

D

és

B_{1}

között van.
Most már ‐

D'

-vel jelölve egy pontot

C B

-nek

B

-n túli meghosszabbításán,

D B C_{1} ∢ = D B D' ∢ = B D C_{1} ∢

, ezért

D C_{1} = B C_{1}

. Másrészt

B_{1} C D ∢ = B C D ∢ = C D B_{1} ∢

, és ezért

C B_{1} = D B_{1} = D C_{1} + C B_{1} = B C_{1} + C B_{1}

, a feladat követelményének megfelelően. A szerkesztés minden (az

A B < A C

feltevésnek megfelelő) háromszögben egyértelműen végrehajtható.
2. Tegyük fel most, hogy

B_{1}

(és vele

C_{1}

) az

A C

, ill.

A B

oldal

A

-n túli meghosszabbításán van (az ábrán

B_{1}^{*}

, ill.

C_{1}^{*}

). A fentihez hasonló meggondolás mutatja, hogy az a

D^{*}

pont, amelyhez úgy jutunk, hogy a

B C_{1}^{*}

szakaszt felmérjük

C_{1}^{*} B_{1}^{*}

-nak

C_{1}^{*}

-on túli meghosszabbítására, azonos az

A B C

háromszög

B

-nél levő belső szöge és

C

-nél levő külső szöge felezőinek metszéspontjával, az

A B C

háromszög

A C

oldalához hozzáírt külső érintőkör középpontjával. Ebből a keresett egyenesre az előbbitől különböző

a_{1}^{*}

megoldást kapjuk. A fentiekhez hasonlóan be lehet ugyanis látni, hogy a most mondott szögfelezők

D^{*}

metszéspontjára nézve

A D^{*} C ∢ + D^{*} C B ∢ < 180^{\circ}

, ezért

D^{*} C_{1}^{*}

A D^{*} C

szögtéren kívül halad, tehát

C_{1}^{*}

A B

oldal

A

-n túli meghosszabbításán van.
3. Más megoldás nincs. Ugyanis

B_{1}

nem lehet

A C

-nek

C

-n túli meghosszabbításán, mert

γ < β

miatt

γ

hegyes szög, egy ilyen

B'_{1} C'_{1} = a'_{1}

helyzettel¹ a

B C B'_{1}

tompaszög, tehát a

B B'_{1} C

és

B B'_{1} C'_{1}

háromszögekből

C B'_{1} < B B'_{1} < B C'_{1} + C'_{1} B'_{1}

, s így a követelmény nem teljesülhet. Ezzel a feladat megoldását befejeztük.
Mészáros György (Budapest, Piarista g. I. o. t.)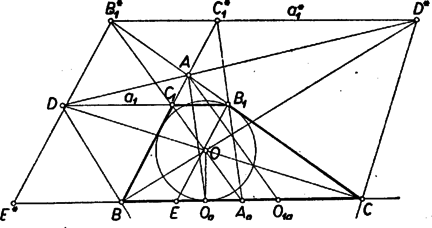

2. ábra

II. megoldás. Messe a

B_{1}

-en, ill.

B_{1}^{*}

-on átmenő,

A B

-vel párhuzamos egyenes

B C

-t

E

-ben, ill.

E^{*}

-ban (2. ábra). Nyilvánvaló, hogy az

A B_{1} C_{1}

B_{1} C E

A B_{1}^{*} C_{1}^{*}

és

B_{1}^{*} C E^{*}

háromszögek hasonlók

A B C

-hez, ezért

\begin{matrix} B C_{1} = E B_{1} = \frac{C B_{1}}{A C} \cdot A B, C_{1}^{*} B_{1}^{*} = \frac{B C_{1}^{*} - A B}{A B} \cdot B C, \\ C_{1} B_{1} = \frac{A C - C B_{1}}{A C} \cdot B C, C B_{1}^{*} = \frac{A C}{A B} \cdot E^{*} B_{1}^{*} = \frac{A C}{A B} \cdot B C_{1}^{*} . \end{matrix}

Ezeket a

B C_{1} + C_{1} B_{1} = C B_{1}

, ill.

B C_{1}^{*} + C_{1}^{*} B_{1}^{*} = C B_{1}^{*}

követelménybe helyettesítve egyismeretlenes egyenletet kapunk

C B_{1}

, ill.

B C_{1}^{*}

-ra, amelyből

\begin{matrix} C B_{1} = \frac{B C \cdot A C}{B C + A C - A B}, ill. B C_{1}^{*} = \frac{B C \cdot A B}{B C + A B - A C} . \end{matrix}

Az adódott nevezők 2-szer akkorák, mint az

A B C

háromszögbe írt kör és a

B C

oldal

O_{a}

érintkezési pontjának

C

-től, ill.

B

-től mért

C O_{a}

B O_{a}

távolsága. Ezért eredményeink ‐ a

B C

oldal felezőpontját

A_{0}

-lal jelölve ‐

\begin{matrix} C B_{1} : C A = C A_{0} : C O_{a}, ill. B C_{1}^{*} : B A = B A_{0} : B O_{a} \end{matrix}

alakban írhatók, és ezek szerint

B_{1}

-et és

C_{1}^{*}

-t

C A

, ill.

B A

-ból az

A_{0}

-n átmenő,

A O_{a}

-val párhuzamos egyenes metszi ki.
A szerkesztés helyességének bizonyítását az olvasókra bízzuk. Mutassák meg azt is, hogy

C_{1} B_{1}^{*}

egyenes is átmegy

A_{0}

-on és párhuzamos

A O_{1 a}

-val, ahol

O_{1 a}

B C

oldalhoz hozzáírt külső érintő körnek

B C

-n levő érintési pontja.
Kiegészítéssel és egyszerűsítéssel a következők dolgozatai alapján:
Tamás Géza (Makó, József A. g. I. o. t.)
és Tihanyi László (Budapest, Petőfi S. g. I. o. t.)

¹Az ábrán

B'_{1}

helyett

B'

áll.