Feladat: 689. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Hirka András ,  Raisz Miklós ,  Szép András 
Füzet: 1961/december, 216 - 218. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorika, Szöveges feladatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1961/március: 689. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A sorrendre (vagyis a nevekre) való tekintet nélkül a 6 rajzszögnek 4 személy között való eloszlására a következő lehetőségek vannak:

a)6,0,0,0;d)4,1,1,0;g)3,1,1,1;b)5,1,0,0;e)3,3,0,0;h)2,2,2,0;c)4,2,0,0;f)3,2,1,0;f)2,2,1,1.

α) Az a), g) és h) lehetőségeket így is mondhatjuk: egy valakié 6, ill. 3, ill. 0 rajzszög, a többiek a maradékon egyenlően osztoznak. Vagy így: valakinek x, a többieknek y számú rajzszöge, van, ‐ ahol persze x+3y=6, és x≠y. Nevezzük az x, y, y, y felsorolást az eloszlás képletének. Az előbbi ,,valaki'' (az x) mindhárom esetben a 4 személy mindegyike lehet, ezért 3⋅4=12 ilyen eloszlás van.
β) A b) c) és d) esetek megegyeznek abban, hogy 2 személynek ugyanannyi rajzszöge van, a másik 2-nek pedig ezektől és egymástól különböző számú rajzszöge, az eloszlás képlete: x, y, z, z, ahol x≠y≠z≠x. Az első olyan személy, akinek a többitől eltérő (x) számú rajzszöge van, 4-féleképpen vehető figyelembe. Ezt változatlanul hagyva a második (az y) a hátralevők közül 3-féleképpen választható. Ezzel már kiadódott, kik a z számú rajzszöggel bírók, tehát a személyek mindhárom esetben 4⋅3=12-féleképpen rendelhetők hozzá az eloszláshoz. Ilyen képletű eloszlás 3⋅12=36 van.
γ) Az e) és j) esetek az előbbiektől csak abban térnek el, hogy x=y. Ezért az előbbiekből 2‐2 lehetőség megegyezik. Pl. ha előbb Péternek volt x, Rezsőnek y, most a ,,Rezső, Péter'' sorrend ugyanazt az eloszlást adja. Így mindkét esetben 12:2=6 lehetőség van, együttvéve 2⋅6=12.
δ) Végül az f) elosztás egyedülálló, csak így lehetséges, hogy mindenkinek más‐más számú rajzszöge legyen. Egymás után kiválasztva a 3, a 2, az 1 rajzszög tulajdonosát, az elsőre 4-, a másodikra 3- és a harmadikra 2-féle kijelölés lehetséges, tehát az ilyen eloszlások száma 4⋅3⋅2=24.
Így az eloszlások száma az α), β), γ), δ) csoportokból 12+36+12+24=84.
 

Hirka András (Pannonhalma, Bencés g. I. o. t.)
 

II. megoldás. Ha csak két fiúról lenne szó, úgy akárhány rajzszögük volna is együttesen, ez mindig a rajzszögek számánál 1-gyel többféleképpen oszolhatna meg köztük. Ugyanis az egyik fiúé lehetne az összes rajzszög, vagy ennél 1-gyel, vagy 2-vel kevesebb, és így tovább, vagy 2; vagy 1, végül az is lehet, hogy egy rajzszög sem az övé. Ebből már mindig látjuk a másik fiú rajzszögeinek számát is.
Hasonlóan feladatunkban a négy fiút előbb csak két párba osztva, a párok között a 6 rajzszög 7-féleképpen oszolhat meg, az első párnak
6,5,4,3,2,1,vagy0(1)
rajzszöge lehet, a fennmaradó
0,1,2,3,4,5,6(2)
rajzszög pedig a második pár tulajdonában van.
Tegyük fel most, hogy Péternek és Rezsőnek együtt 4 rajzszöge van, tehát a másik kettőre együttvéve 2 marad. Az első párban 5-, a másodikban 3-féle eloszlás lehetséges, és mivel az első pár mindegyik eloszlása összekapcsolódhat a második pár mindegyik eloszlásával, azért feltevésünk mellett a 4 fiú között 5⋅3=15 eloszlás lehetséges.
Végigmenve az (1) és (2) valamennyi két párra osztott lehetőségén a 4 fiúra
7⋅1+6⋅2+5⋅3+4⋅4+3⋅5+2⋅6+1⋅7=84
eloszlási lehetőséget kapunk.
 

Szép András (Budapest Rákóczi F. g. I. o. t.)
 
III. megoldás. Gondoljuk ábrázolva az eloszlási lehetőségeket a következők szerint. Rajzoljunk mindegyik fiú neve mellé annyi egységnyi hosszú (vízszintes) szakaszt, ahány rajzszöge van, ha pedig nincs rajzszöge, akkor egy 0 hosszúságú szakaszt (vagyis egy pontot). Illesszük ezeket egymás alá, ugyancsak egységnyi távolságban, majd Rezsőtől kezdve toljuk mindegyik szakasz kezdőpontját a megelőzőnek a végpontja alá.
 
 
1. ábra
 

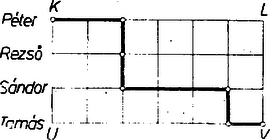Így Tamás szakaszának V végpontja 6 egységgel jobbra és 3 egységgel lefelé van Péter szakaszának K kezdőpontjától. Ábráinkat négyzethálós papíron készítve és a szomszédos szakaszpárok vég- és kezdőpontját összekötve egy‐egy csupa hálózati egyenesen haladó, mindig vagy jobbra, vagy lefelé irányuló útvonalat kapunk K-tól V-ig. A feladat szövegében említett eloszlási példát az 1. ábra ábrázolja.
Más eloszláshoz más ilyen útvonal tartozik, és megfordítva minden olyan K és V közti útvonalhoz, amely az 1. ábra KLVU téglalapjának kerületén vagy belső hálózati szakaszain halad, tartozik eloszlás.
Így csak azt kell megállapítanunk, hányféleképpen juthatunk el K-ból V-be a mondott feltételek megtartásával. Ezt a 2. ábra csomópontjaihoz az odavezető rész‐utak számának beírásával kapjuk.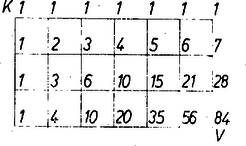
 
 
2. ábra
 

Az első sor és az első oszlop minden csomópontjához csak irányváltozás nélkül, 1-féleképpen juthatunk el. Minden további csomóba akár a fölötte, akár a tőle balra álló csomóból érkezhetünk, ezért az ideérkezési lehetőségek száma egyenlő az amazokhoz írt számok összegével. Így V-hez 84 út vezet, ennyi eloszlás lehetséges.
 

Raisz Miklós (Miskolc, Földes F. g. II. o. t.)