Kezdőlap


Feladat:	687. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Lukács Lídia , Strommer Richárd
Füzet:	1961/december, 214. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Hozzáírt körök, Beírt kör középpontja, Gyakorlat
Hivatkozás(ok):	Feladatok: 1961/február: 687. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a háromszög beírt körének középpontja $O$ , és a $B C$ oldalhoz hozzáírt kör középpontja 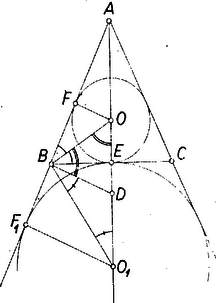$O_{1}$ .

Nyilvánvaló, hogy mindkét kör

E

-ben érinti

B C

-t, ezért a következőket kell bizonyítanunk

\begin{matrix} B D - E D = O E, & (1) \\ B D + E D = O_{1} E . & (2) \end{matrix}

(1)-et átrendezve

B D = O E + E D = O D

, ami azt jelenti, hogy a

D B O

háromszög egyenlő szárú. Ezt fogjuk bizonyítani. ‐

B O

felezi az

A B C

szöget, ezért

\begin{matrix} D B 0 ∢ = 90^{\circ} - A B O ∢ = 90^{\circ} - E B O ∢ = E O B ∢ - D O B ∢ . \end{matrix}

Ebből következik állításunk.
Hasonlóan (2)-ből

B D = O_{1} E - E D = O_{1} D

, tehát elegendő bebizonyítani, hogy a

D B O_{1}

háromszög egyenlő szárú. ‐

B O_{1}

felezi az

A B C

szög külső szögét, ezért merőleges

B O

-ra. Így az előbbi egyenlőség felhasználásával:

\begin{matrix} D B O_{1} ∢ = O B O_{1} ∢ - D B O ∢ = 90^{\circ} - D O B ∢ = 90^{\circ} - O_{1} O B ∢ = O O_{1} B ∢ = \\ = D O_{1} B ∢, \end{matrix}

amiből állításunk következik.

Lukács Lídia (Püspökladány, Karacs F. g. I. o. t.)

II. megoldás. Érintsék a körök az

A B

egyenest

F

, ill.

F_{1}

-ben, így

O F ∥ O_{1} F_{1} ∥ D B

. A

B

-ből a körökhöz húzott érintőszakaszok egyenlőségéből

B F = B E = B F_{1}

, ezért

B D

F O O_{1} F_{1}

trapéz középvonala, és így felezi az

O O_{1}

szárat:

\begin{matrix} O_{1} F_{1} + O F = O_{1} E + O E = 2 \cdot B D, és \\ O_{1} D - O D = (O_{1} E - E D) - (O E + E D) = 0, amiből \\ O_{1} E - O E = 2 \cdot E D . & (4) \end{matrix}

Most már (3) és (4)-ből kivonással (1), összeadással (2) adódik.

Strommer Richard (Budapest, Piarista g. I. o. t.)