Kezdőlap


Feladat:	651. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ámon Magdolna , Bana S. , Baróti Gy. , Bor Edit , Corrádi G. , Dévényi l. , Dobó F. , Draskovits P. , Fazekas P. , Fekete S. , Fraknói Z. , Gáspár Hedvig , Glósz L. , Gönczy J. , Helyes Margit , Hunyadi Magdolna , Jahn L. , Kádár L. , Kádár Levente , Kántor L. , Kászonyi L. , Keviczky László , Kiss Gábor , Koós I. , Krokos J. , Lehel Cs. , Lehel J. , Major J. , Markó J. , Meggyessy Veronika , Nagy Angéla , Papp M. , Rácz L. , Rejtő Lídia , Sütő Katalin , Szepesvári Gy. , Szidarovszky F. , Szigeti F. , Tamás E. , Tasnády Mária , Tóth Á. , Varga Virág , Verdes M.
Füzet:	1961/szeptember, 19 - 21. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/október: 651. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Bizonyításunkat az 1. ábrán látható helyzethez kapcsoljuk; $e$ , $f$ , $g$ és $P$ más kölcsönös helyzetében az állítás hasonlóan bizonyítható.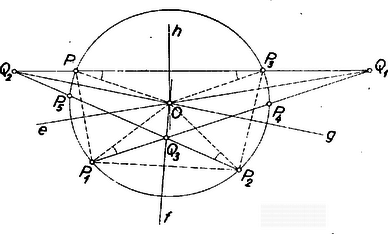

1. ábra

Q_{1} P_{1}

, és

Q_{2} P_{2}

metszéspontját

Q_{3}

-mal jelölve elég belátnunk, hogy a

P_{1} P_{2} Q_{3} ▵

egyenlő szárú:

Q_{3} P_{1} = Q_{3} P_{2}

; így ugyanis

Q_{3}

P_{1} P_{2}

szakasz felező merőlegesén van, ami pedig a tükrözésnél fogva az

f

egyenes. ‐ Már most a tükrözés folytán

O P = O P_{1} = O P_{2} = O P_{3}

, tehát az

O P P_{3} ▵

egyenlő szárú, és

h

tengelye átmegy

O

-n. Így az

\begin{matrix} O P_{1} Q_{3}, O P_{1} Q_{1}, O P Q_{1}, O P P_{3}, O P_{3} P, O P_{3} Q_{2}, O P_{2} Q_{2}, O P_{2} Q_{3} \end{matrix}

szögek sorozatában (a 2-iktól kezdve) mindegyik egyenlő az előtte állóval, mert váltakozva vagy csupán ugyanazon szögnek más jelöléssel való megadásáról van szó, vagy a szomszédos szögek egymásnak rendre

e

h

g

-re tükörképei. Innen

O P_{1} Q_{3} ∢ = O P_{2} Q_{3} ∢

, az

O P_{1} P_{2}

egyenlő szárú háromszögből

O P_{1} P_{2} ∢ = O P_{2} P_{1} ∢

, ezekből kivonással

Q_{3} P_{1} P_{2} ∢ = Q_{3} P_{2} P_{1} ∢

, tehát a

Q_{3} P_{1} P_{2} ▵

valóban egyenlő szárú.

Kádár Levente (Mezőkövesd, I. László g. II. o. t.)

Megjegyzés. Lényegében ugyanezt a bizonyítást mondjuk el más szavakkal, ha arra hivatkozunk, hogy

P P_{1} P_{2} P_{3}

húrnégyszög (hurkolt is lehet), és a

P P_{1} Q_{1}

P_{2} P_{3} Q_{2}

háromszögek egyenlő szárúak.

Keviczky László (Ráckeve, Ady E. g. II. o. t.)

II. megoldás. Folytassuk a tükrözést, és legyen

P_{3}

képe

e

-re

P_{4}

P_{4}

képe

f

-re

P_{5}

, és

P_{5}

képe

g

-re

P_{6}

. Ekkor

P_{6}

egybeesik

P

-vel. Ismeretes ugyanis, hogy két metsző tengelyen való egymás utáni tükrözés eredményét az a forgatás is megadja, melynek középpontja a tengelyek közös pontja, szöge pedig 2-szer akkora és olyan forgási irányú, mint az 1. tengelyt a 2-ba vivő forgás (lásd a 2‐3. ábrán a

Q

pontok átvitelét

Q^{*}

-ba; állításunk akkor is érvényes, ha

t_{1}

-et ellentétes irányban, tompa szöggel forgatjuk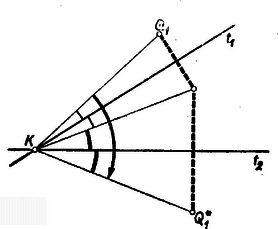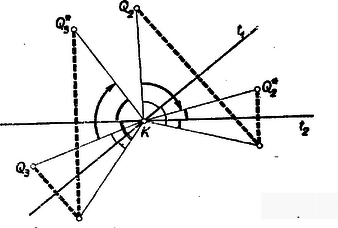

t_{2}

,-be).

2. ábra

3. ábra

Eszerint a 6 tükrözés eredménye helyettesíthető 3 forgatással az

O

körül és a forgatás szöge rendre az

e

-t

f

-be,

g

-t

e

-be és

f

-et

g

-be vivő forgatás 2-szerese. E 3 forgatás összege egyetlen forgatás

O

körül. A 3-ik forgatást 2-iknak véve, a 3 forgás összege annyi, amennyi

e

-t

e

-be viszi, ezért értéke

180^{\circ}

, vagy

360^{\circ}

(4. ábra), így kétszerese

360^{\circ}

, vagy

720^{\circ}

, tehát valóban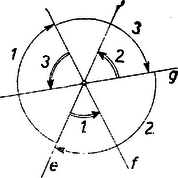

P_{6} = P

4. ábra

Megmutatjuk, hogy a kérdéses

Q_{3}

pont a

P_{1} P_{4}

és

P_{2} P_{5}

egyenesek közös pontja. Ugyanis

P_{4}

és

P_{3}

tükrösek

e

-re, ezért

P_{3}

-on átmenő

Q_{1} P

-nek

e

-re vett

Q_{1} P_{1}

tükörképe átmegy

P_{4}

en, másrészt

Q_{1} P_{1}

Q_{3}

egyik meghatározója, tehát

P_{1} P_{4}

átmegy

Q_{3}

-on. Ugyanígy

P_{5}

és

P

tükrösek

g

-re, ezért a

P

-n átmenő

Q_{2} P_{3}

-nak

g

-re vett

Q_{2} P_{2}

tükörképe átmegy

P_{5}

-ön, másrészt

Q_{3}

-on, tehát

P_{2} P_{5}

átmegy

Q_{3}

-on. És mivel

P_{1}

és

P_{2}

, valamint

P_{4}

és

P_{5}

pontok az

f

-re tükrösek, ezért ez áll a

P_{1} P_{4}

és

P_{2} P_{5}

egyenesekre is, így pedig közös

Q_{3}

pontjuk

f

-en van.

Kiss Gábor (Debrecen, Kossuth L. gyak g. II. o. t.).

Megjegyzés. Biztosra vettük, hogy

Q_{1} P_{1}

és

Q_{2} P_{2}

nem párhuzamosak, a

Q_{3}

pont létezik. Tekintsük most a

Q_{1} Q_{3} Q_{2}

szöget.

e

f

g

felezi a

Q_{1} Q_{3} Q_{2} ▵

szögeit. Így az

O Q_{1} Q_{2} ▵

szögeit rendre

ω

φ_{1}

φ_{2}

-vel jelölve

Q_{1} Q_{3} Q_{2} ∢ = 180^{\circ} - 2 φ_{1} - 2 φ_{2} = 2 ω - 180^{\circ}

. Eszerint

ω = 90^{\circ}

, más szóval

e ⊥ g

esetén a

Q_{1} Q_{2} Q_{3} ▵

nem jön létre,

Q_{1} P_{1}

és

Q_{2} P_{2}

párhuzamosak

f

-fel. ‐ Akkor is elfajult eset adódik, ha a

P P_{3}

egyenes átmegy

O

-n, továbbá, ha

P_{1}

éppen

f

-en adódik. Ilyenkor nincs mit bizonyítani, mert

Q_{1} \equiv Q_{2} \equiv = O

, ill.

P_{2} \equiv P_{1}

, és így

Q_{3}

O

-ba, ill.

P_{1}

-be esik, ami valóban

f

-en van. Ha pedig

P

e

-n van, továbbá, ha

P_{3}

éppen

g

-n adódik, akkor egyeneseink egyike határozatlan.