Kezdőlap


Feladat:	639. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baróti Gy. , Egyed Julianna , Endreffy Z. , Fajszi Cs. , Farkas Z. , Gálfi l. , Góth L. , Kászonyi L. , Katona Éva , Katona Mária , Kiss Tünde , Kóta J. , Kunszt Z. , Lehel J. , Majoros László , Máté A. , Máté E. , Nagy Dénes L. , Németh I. , Nováky B. , Opálény M. , Patthy l. , Pellionisz A. , Pór A. , Raisz M. , Sebestyén Z. , Simonovits M. , Sonnevend Gy. , Szepesvári I. , Tasnády Mária , Tószegi S. , Vesztergombi Gy. , Zalán P.
Füzet:	1961/április, 162 - 163. oldal		PDF \| MathML
Témakör(ök):	Magasságpont, Szinusztétel alkalmazása, Síkgeometriai számítások trigonometriával, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/május: 639. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Elég az állítást a szokásos jelölésekkel pl. az $A M$ távolságra megmutatni, vagyis hogy 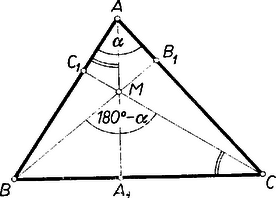$A M = a ctg α$ , ha $α \leq 90^{\circ}$ , és $A M = a ctg (180^{\circ} - α)$ , ha $α > 90^{\circ}$ .
Ha $α < 90^{\circ}$ , akkor $β$ és $γ$ -nak legalább az egyike szintén hegyesszög, legyen ez $β$ . Ekkor $C$ -nek az $A B$ egyenesre való $C_{1}$ vetülete ‐ ami egyszersmind $M$ vetülete is ‐ $A$ és $B$ közé esik, és $ctg α = A C_{1} / C C_{1}$ (1. ábra).

1. ábra

M A C_{1}

és

B C C_{1}

derékszögű háromszögek hasonlók, mert

A

, ill.

C

-nél levő (hegyes) szögük szárai páronként merőlegesek. Így

M A : A C_{1} = B C : C C_{1}

, ebből pedig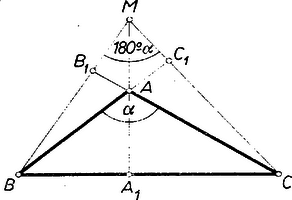

\begin{matrix} M A = B C \frac{A C_{1}}{C C_{1}} = B C ctg α . \end{matrix}

2. ábra

Ha pedig

α > 90^{\circ}

(2. ábra), akkor ‐ mint a 637. gyakorlat¹ megoldásában láttuk ‐ az

M B C

háromszög hegyesszögű, és magasságpontja

A

, és így az előző eset szerint

A M = B C ctg α'

, ahol

α'

B M C

szöget jelöli. Ez pedig egyenlő a külső szögével,

180^{\circ} - α

-val, ugyanis az

M B_{1} A C_{1}

négyszögben szemben fekszik a csúcsszögével, és összegükre

180^{\circ}

marad, mert a szemben fekvő

B_{1}

és

C_{1}

-nél levő szögek összege szerkesztésnél fogva két derékszög.
Végül

α = 90^{\circ}

esetén egyrészt

M

A

-ba esik, így

M A = 0

, másrészt

ctg α = 0

, tehát az állítás ekkor is igaz.

Majoros László (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

A dolgozatoknak kb. fele két szög függvényeit és a szinusz-tételt használta fel ‐ esetleg burkoltan ‐ vagyis a szükségesnél erősebb eszközökkel dolgozott. Közülük több ún. második megoldás. Márpedig egyszerűbb megoldás után egy bonyolultabb második megoldásnak nincs értéke; az ilyenre többnyire nem adunk külön pontot. A következő megoldás a trigonometriából ismét csak a

90^{\circ}

-nál nem nagyobb szög kotangensének meghatározását használja fel.

II. megoldás: Megmutatjuk az állítás helyességét

M

-nek egy hegyesszögű és egy tompaszögű csúcstól való távolságára. Feltehetjük, hogy

β

hegyesszög. Tekintsük a háromszög körülírt körében a

B

-ből kiinduló átmérő másik végpontját,

B^{*}

-ot. Thalész tétele szerint

B^{*} A ⊥ B A

, tehát

B^{*} A ∥ C M

; hasonlóan

B^{*} C ∥ A M

, így az

A M C B^{*}

négyszög paralelogramma,

A M = B^{*} C

, és

C 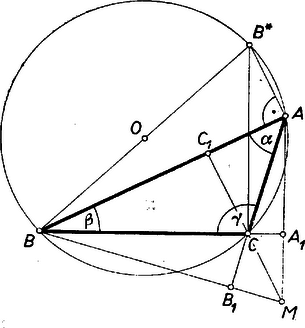M = B^{*} A

(3. ábra).

3. ábra

Hegyesszög esetén, mint ábránkon

α

, a

B^{*}

ugyanazon a

B C

íven van, mint

A

, ezért

B B^{*} C ∢ = α

, és így a

B B^{*} C

derékszögű háromszögből

A M = B^{*} C = B C ctg α

.
Tompaszög esetén pedig, mint ábránkon

γ

, a

B^{*}

C

-t nem tartalmazó

A B

íven van, ezért

B B^{*} A ∢ = 180^{\circ} - γ

(hegyesszög), és így a

B B^{*} A

derékszögű háromszögből

C M = B^{*} A = B A ctg (180^{\circ} - γ)

¹Lásd K. M. L. 22 (1961) 110. o.