Kezdőlap


Feladat:	637. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baróti Gy. , Csákó Gy. , Dobó F. , Endreffy Z. , Fajszi Cs. , Farkas Z. , Gálfi l. , Katona Éva , Kóta J. , Kunszt Z. , Kövessi Ágnes , Lehel J. , Máté A. , Máté E. , Nagy Géza , Németh I. , Nováky B. , Raisz M. , Sebestyén Z. , Simonovits M. , Sólyom Ilona , Tasnády Mária , Vesztergombi Gy. , Zalán P.
Füzet:	1961/március, 110 - 112. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/május: 637. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Állapítsuk meg általában, hogy milyen összefüggés áll fenn egy tetszés szerinti $A B C$ háromszög és az ennek $A_{1} B_{1} C_{1}$ talpponti háromszöge szögei között. Ebben felhasználjuk, hogy bármelyik oldal két végpontjából kiinduló magasságok talppontjai rajta vannak az illető oldal mint átmérő fölé írt Thalész‐körön, így e négy pont húrnégyszöget határoz meg.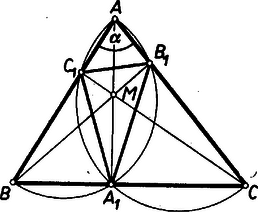
Hegyesszögű háromszög esetén (1. ábra) mindhárom talppont a megfelelő oldal belsejében van, így pl. az $A A_{1}$ magasság a $B_{1}$ , $C_{1}$ talppontokat szétválasztja, és ezért a $B_{1} A_{1} C_{1}$ szög a $B_{1} A_{1} A$ és $A A_{1} C_{1}$ szögek összege.

1. ábra

A B

és

A C

átmérők fölötti Thalész‐körben a kerületi szögek tétele alapján

\begin{matrix} B_{1} A_{1} A ∢ = B_{1} B A ∢ = 90^{\circ} - α, A A_{1} C_{1} ∢ = A C C_{1} = 90^{\circ} - α, \end{matrix}

és így

B_{1} A_{1} C_{1} ∢ = 180^{\circ} - 2 α

. Hegyesszögű háromszög talpponti háromszögének szögei rendre egyenlők az eredeti háromszög szögei pótszögeinek 2-szeresével.
Tompaszögű háromszög

M

magasságpontja kívül esik a háromszögön ‐ a 2. ábrán

B A C ∢ = α > 90^{\circ}

‐ és

M

A

-ból húzott magasságnak a csúcson, a

B

és

C

-ből húzott magasságnak pedig a talpponton túli meghosszabbításán van.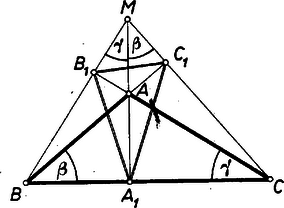

2. ábra

Így

M

a hegyesszögek

B

C

csúcsával hegyesszögű háromszöget alkot, ‐ ugyanis

\begin{matrix} M B C ∢ = B_{1} B C ∢ = 90^{\circ} - γ < 90^{\circ}, ugyanígy M C B ∢ = 90^{\circ} - β < 90^{\circ}, és \\ B M C ∢ = B M A_{1} ∢ + A_{1} M C ∢ = γ + β = 180^{\circ} - α < 90^{\circ}, \end{matrix}

és az

M B C

háromszög talpponti háromszöge egybeesik az

A B C

háromszögével, az

M

B

és

C

-ből húzott magasság talppontja rendre

A_{1}

C_{1}

B_{1}

. Így az előzők alapján:

\begin{matrix} B_{1} A_{1} C_{1} ∢ & = 180^{\circ} - 2 B M C ∢ = 180^{\circ} - 2 (180^{\circ} - α) = 2 α - 180^{\circ}, \\ A_{1} B_{1} C_{1} ∢ & = 180^{\circ} - 2 M C B ∢ = 180^{\circ} - 2 (90^{\circ} - β) = 2 β, \\ A_{1} C_{1} B_{1} ∢ & = 180^{\circ} - 2 M B C ∢ = 180^{\circ} - 2 (90^{\circ} - γ) = 2 γ . \end{matrix}

Eszerint tompaszögű háromszög talpponti háromszögének két szöge

2

-szer akkora, mint az eredeti háromszög megfelelő hegyes szöge, a harmadik pedig

180^{\circ}

-kal kisebb a tompaszög

2

-szeresénél.
(Derékszögű háromszögben a magasságtalppontok nem alkotnak valódi háromszöget.)
Mármost az adott

H

háromszög tompaszögű, mert első két szögének összege kisebb a harmadiknál. Egyszerűség kedvéért legyen a legkisebb szög

δ

, ekkor a további kettő

2 δ

4 δ

, és összegük

7 δ = 180^{\circ}

. Így a fentiek szerint

T_{1}

-ben

A_{1}

-nél

2 δ

B_{1}

-nél

4 δ

C_{1}

-nél pedig

8 δ - 180^{\circ} = δ

nagyságú szög van. Így

H

és a belőle leszármaztatott

T_{1}

hasonlók, mert szögeik egyenlő párokba kapcsolhatók. Ebből következik, hogy

T_{1}

és a belőle ugyanazon eljárással‐leszármaztatott

T_{2}

is hasonlók, tehát

T_{2}

H

-hoz is hasonló. Ugyanígy

H

-nak bármely sorszámú talpponti háromszöge hasonló

H

-hoz (3. ábr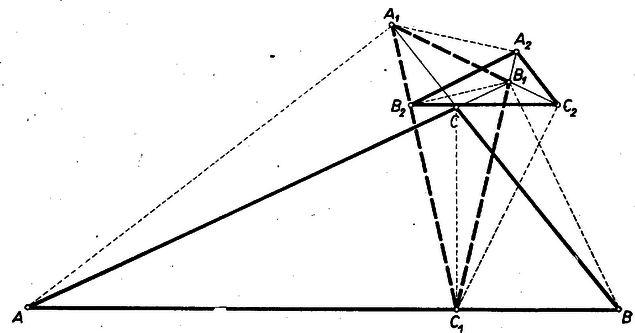a).

3. ábra

Megmutatjuk, hogy

T_{2}

és

H

-nak

B_{2} C_{2}

és

A B

oldala párhuzamos. Ehhez elég belátni, hogy

C_{2} B_{2} C_{1}

és

A_{1} C_{1} A

váltószögek, vagyis a

B_{2} C_{2}

és

C_{1} A

félegyenesek

T_{1}

megfelelő

C_{1} A_{1} = b_{1}

oldalának

C_{1} B_{2}

szakaszával ugyanakkora szöget zárnak be, továbbá hogy

b_{1}

-nek ellentétes oldalán vannak. E két szöget meghatározó ponthármasok szerkesztésüknél fogva egymás megfelelői. Ugyanis a fenti két hasonlóságot így is kimondhatjuk: a

T_{1}

és

T_{2}

hat csúcsából álló pontrendszer hasonló a

H

és

T_{1}

hat csúcsából álló pontrendszerhez. És mivel

H

és

T_{1}

hasonlóságában

A

B

C

-nek rendre az ugyanakkora szög

C_{1}

A_{1}

B_{1}

csúcsa felel meg, ugyanígy

T_{1}

és

T_{2}

hasonlóságában

A_{1}

B_{1}

C_{1}

-nek sorra

C_{2}

A_{2}

B_{2}

, azért a

T_{1}

T_{2}

rendszer

\begin{matrix} A_{1}, B_{1}, C_{1}, A_{2}, B_{2}, C_{2} \end{matrix}

csúcsai egymás után a

H

T_{1}

, rendszer

\begin{matrix} B, C, A, B_{1}, C_{1}, A_{1} \end{matrix}

csúcsainak felelnek meg, és így valóban

C_{2} B_{2} C_{1} ∢ = A_{1} C_{1} A ∢

. ‐

C_{1}

A B

szakaszon van,

A_{1}

pedig

B C

-nek

C

-n túli meghosszabbításán, ezért

B

és

C

b_{1}

-nek

A

-val ellentett oldalán vannak, továbbá

B_{1}

és

C_{2}

is, mert

B_{1}

A C

oldal

C

-n,

C_{2}

pedig az

A_{1} B_{1}

oldal

B_{1}

-en túli meghosszabbításán van; eszerint

B_{1}

valóban szétválasztja

A_{1}

-et és

C_{2}

-t. Így fennáll, hogy

B_{2} C_{2} ∥ A B

. ‐ Hasonlóan

C_{2} A_{2} ∥ B C

. Végül

B_{2} A_{2} B_{1} ∢ = C_{1} B_{1} C ∢

, továbbá

B_{2}

és

C

B_{1} C_{1}

egyenes ugyanazon oldalán vannak, ezért a szögek egyállásúak:

A_{2} B_{2} ∥ C A

. Ezzel a bizonyítást befejeztük.
A

G

háromszög egyenlő szárú és tompaszögi, mert kisebb szögeit

ε

-nal jelölve a nagyobb

8 ε

, és ez nagyobb

ε + ε

-nál. Így a szögek összegéből

10 ε = 180^{\circ}

. Talpponti háromszögének,

U_{1}

-nek szögei

2 ε

2 ε

és

16 ε - 180^{\circ} = 6 ϵ

, így ez is tompaszögű, ennélfogva második talpponti háromszögének,

U_{2}

-nek szögei

4 ε

4 ε

2 ε

, ez tehát hegyesszögű. Továbbmenve

U_{2}

első két szöge

180^{\circ} - 8 ε = 2 ϵ

, a harmadik

180^{\circ} - 4 ε = 6 ε

, vagyis

U_{3}

hasonló

U_{1}

-hez és hasonlóan

U_{4}

hasonló

U_{2}

-höz. Így

G

minden páratlan sorszámú talpponti háromszöge

U_{1}

-hez hasonló, a páros sorszámúak pedig

U_{2}

-höz, tehát egyik sem hasonló

G

-hez.

Kövessi Ágnes (Budapest, Szilágyi Erzsébet lg. II. o.t.)