Kezdőlap


Feladat:	631. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bácskai F. , Benczúr A. , Endreffy Z. , Fajszi Cs. , Farkas Z. , Fazekas P. , Felszeghy Tamás , Gálfi l. , Gerlicze Éva , Góth L. , Kászonyi L. , Katona Mária , Kóta J. , Máté A. , Mezei M. , Nádasdy G. , Nováky B. , Opálény M. , Pór A. , Raisz M. , Sebestyén Z. , Sólyom Iona , Somfalvi József , Sonnevend Gy. , Strobl Ilona , Tóth Edit , Várkonyi S. , Vesztergombi Gy.
Füzet:	1961/február, 71 - 72. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/április: 631. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tekintsük a feladatot megoldottnak, és legyen a keresett háromszög $A B C$ , ebben $B C = a$ , $B A C ∢ = α$ és $B B_{0} = s_{b}$ adottak, ahol $B_{0}$ a $C A$ oldal felezőpontja (1. ábra).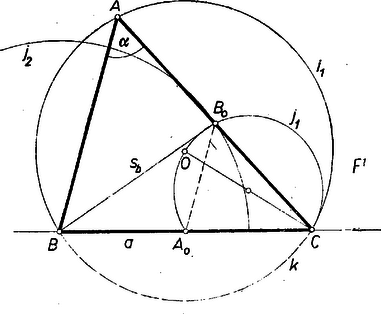

1. ábra

a

és

α

A

csúcs számára előírnak egy mértani helyet: az

a

szakasz

α

nyílásszögű látószög-körívpárjának pontjait. Mivel azonban a

B C

oldal elhelyezése után még megválaszthatjuk, hogy az

A

csúcsot a

B C

egyenessel kettévágott sík melyik félsíkján kívánjuk kapni ‐ legyen ez

F_{1}

‐, azért

A

mértani helye gyanánt elég a látószög-körívpár

F_{1}

-en levő

i_{1}

tagját figyelembe vennünk. Az

i_{1}

ív az

A B C

háromszög

k

körülírt körének része, és így

i_{1}

-gyel megkaptuk

k

-nak

O

középpontját.
Egyrészt

O

-val, másrészt

s_{b}

alapján

B_{0}

számára két mértani helyet ismerünk. Ugyanis

O B_{0}

merőleges

C A

-ra, vagyis

C B_{0}

-ra ezért

B_{0}

O C

átmérő fölötti Thalész-körön van, pontosabban ennek

F_{1}

-re eső

j_{1}

-ívén. Másrészt

B_{0}

B

körül

s_{b}

sugárral írt körön van, pontosabban

e

körnek

F_{1}

-re eső

j_{2}

ívén.
Ezek alapján megszerkeszthetjük

B_{0}

-t, ezután pedig

A

-t

i_{1}

-ből a

C B_{0}

egyenes metszi ki.
A szerkesztésből nyilvánvaló, hogy a kapott

B C A

háromszög megfelel a követelményeknek. A

j_{1}

és

j_{2}

körívek ‐ akárcsak két kör ‐ legfeljebb

2

pontban metszik egymást, így a megoldások száma a metszéspontok száma szerint

2

1

vagy

0

Felszeghy Tamás (Debrecen, Kossuth L. Gyak. Gimn. II. o. t.)

Megjegyzés. A

j_{1}

ívet úgy is tekinthetjük, hogy az az

i_{1}

-nek a

C

középpontból

2 : 1

arányban való kicsinyítettje. Ezért

B C

-n levő

A_{0}

végpontja felezi

B C

-t,

A_{0} B_{0}

a háromszög középvonala, tehát

A_{0} B_{0} C ∢ = α

. Így

j_{1}

B C

oldal felének,

A_{0} C

-nek

α

nyílású látszögköríve.

Tóth Edit (Székesfehérvár, Vasvári P. lg. II. o. t.)

II. megoldás: Tükrözzük a háromszöget

B_{0}

-ra; így

C

és

A

egymásnak tükörképei, legyen továbbá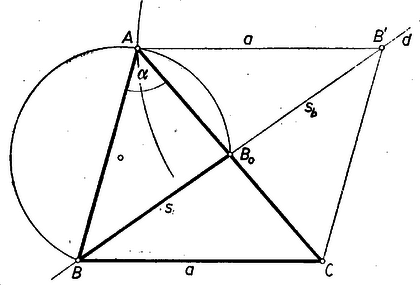

B

képe

B'

2. ábra

Így egyrészt

B B' = 2 s_{b}

másrészt a

B C B' A

négyszög paralelogramma, tehát

B' A = C B = a

, végül

B A B_{0} ∢ = α

.
Ezek alapján a szerkesztés: egy

d

egyenesre egymás után felmérjük a

B B_{0} = B_{0} B' = s_{b}

szakaszokat, a

B B_{0}

fölött

d

egyik oldalán előállítjuk az

α

nyílásszögű látószögkörívet, ezt

B'

körüli

α

sugarú körrel metszve kapjuk

A

-t, végül

A

-nak

B_{0}

-ra való tükörképe

C

Somfalvi József (Budapest, I. István Gimn. I. o. t.)