Feladat: 630. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Csepella Imre ,  Zalán F. Árpád 
Füzet: 1961/február, 70 - 71. oldal  PDF  |  MathML 
Témakör(ök): Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1960/április: 630. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Megmutatjuk, hogy az ABCDE=P ötszög minden csúcsánál ugyanakkora szög van. Eszerint az ötszög szabályos, mert szabályos sokszögnek az olyan konvex sokszöget nevezzük, amelynek valamennyi oldala, továbbá valamennyi szöge egyenlő.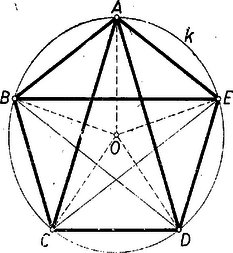

 
 

A B, E, A csúcsnál levő szögek egyenlők. Ezek ugyanis egyszersmind az ACB, ADE, ill. BEA háromszögnek is szögei. E háromszögek egybevágók, mert egy oldaluk a feltevésben szereplő AC, AD, ill. BE átló, további két oldaluk pedig P-nek két oldala, így bármelyik két háromszög oldalai páronként egyenlők. A tekintetbe vett szögek a háromszögeknek az említett átlókkal szemben fekvő szögei, tehát egyenlők.
P-nek C és D-nél levő szögei is egyenlők, mert a CA, DA átlók két-két páronként egyenlő részre osztják őket. Ugyanis egyrészt az előbbi egybevágóságok folytán BCA∢=EDA∢, másrészt a CDA háromszög egyenlőszárú, így ACD∢=ADC∢, ezért összeadással valóban BCD∢=EDC∢.
Végül P-nek a B és D-nél levő szögei is egyenlők. Meghúzva ugyanis a BD átlót egyrészt a BDA és DBE háromszögek egybevágók, mert BD oldaluk közös, további oldalaik pedig a feltevés szerint egyenlők, ezért ABD∢=EDB∢; másrészt a BDC háromszög egyenlő szárú, DC=BC, és ezért DBC∢=BDC∢. Így összeadással ABC∢=EDC∢, amit bizonyítani akartunk. Ezek szerint
AED∢=EAB∢=ABC∢=EDC∢=BCD∢.
Ezzel az állítást bebizonyítottuk.
 

Csepella Imre (Szeged, Radnóti M. Gimn. II. o. t)
 

II. megoldás: Megmutatjuk, hogy az ABCDE=P ötszög köré k kör írható. Így ‐ k középpontját O-val jelölve ‐ az AOB, BOC, COD, DOE, EOA háromszögek egybevágók, O-nál levő szögeik egyenlők. Ezeket ω-val jelölve P bármely csúcsából a további 4 csúcs közti 3 oldal a kerületi és középponti szögek tétele alapján ω/2 szögben látszik. Ezért P mindegyik szöge 3ω/2.
Mármost az ABC és ABE egyenlőszárú háromszögek fentebb látott egybevágósága folytán ACB∢=AEB∢=ε, és így C és E az AB szakasz ε nyílásszögű látószög-körívén van, vagyis A, B, C, E egy k1 kör pontjai. Ugyanígy az AE szakasz B és D-ből ε szögben látszik, ezért E, A, B, D egy k2 kör pontjai. E két kör pedig azonos, mert A, B és E pontjaik közösek. A további C, ill. D pontokkal P minden csúcsáról beláttuk, hogy rajta van e körön. Ezzel az állítást bebizonyítottuk.
 

Zalán F. Árpád (Aszód, Petőfi S. Gimn. II. o. t.)