Feladat: 627. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Ámon Magda ,  Benczúr A. ,  Csákó György ,  Csepella I. ,  Dobó F. ,  Draskóczy Judit ,  Fajszi Cs. ,  Farkas Z. ,  Felszeghy T. ,  Fischer A. ,  Gáspár R. ,  Gyaraki K. ,  Gönczy J. ,  Görbe T. ,  Hőke S. ,  Horváth K. ,  Katona Mária ,  Kerényi Ilona ,  Kiss Gábor ,  Kóta J. ,  Kunszt Z. ,  Kövessi Ágnes ,  Lehel J. ,  Lepsényi Edit ,  Majoros L. ,  Mikes Endre ,  Nagy Dénes ,  Nagy Géza ,  Nováky B. ,  Opálény M. ,  Patthy l. ,  Pellionisz A. ,  Pór A. ,  Raisz M. ,  Sebestyén Z. ,  Seprődi L. ,  Simonovits M. ,  Sólyom Ilona ,  Sonnevend Gy. ,  Szidarovszky Ágnes ,  Szidarovszky F. ,  Szilágyi Mária ,  Tasnády Mária ,  Tóth A. ,  Tóth V. ,  Vesztergombi Gy. ,  Zalán P. 
Füzet: 1961/január, 22 - 25. oldal  PDF  |  MathML 
Témakör(ök): Nomogramok, Gyakorlat
Hivatkozás(ok):Feladatok: 1960/április: 627. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Figyeljük meg a megadott ábrák következő tulajdonságait: Mindegyik skála egyenletes, egymástól legfeljebb az egységszakasz hosszában és a skála irányításában különböznek. Így valamennyi skála alkalmas az egyenes egy szakasza hosszának az illető skála egységében való megmérésére, evégett csupán a végpontokhoz írt skálaértékek különbségét kell vennünk. Pl. GB hossza a V-skálán 14-0=14 egység, az U-skálán 0-(-1,4)=1,4 egység; JD hossza a T-skálán 7,5-3=4,5 egység, az S-skálán 2,5-0,25=2,25 egység. Továbbá mindegyik részfeladatban szereplő három skála olyan egymással párhuzamos egyeneseken fekszik, melyek közül a középső egyenlő távolságra van a szélsőktől; így ha a szélső skálákon két pontot választunk, akkor az ezekkel és e két skála 0-pontjával meghatározott trapéz középvonala a középső skálára esik.
1. Az X-, Y-, Z-skálahármas és az xy¯ egyenes esetében tekintsük az AFKE trapézt, és ennek HC középvonalát. A skálák 0-pontjai az FK egyenesen vannak, egységeik egyenlők, irányításuk megegyező. Ha A és E az X-, ill. Y-skála pozitív felén van, akkor ugyanez áll C-re, és FA=x, KE=y, HC=z, tehát valóban

z=HC=FA+KE2=x+y2.(1)
Az állítás akkor is érvényes, ha A és E mindegyike a skálák negatív felén van. Ekkor C is a Z-skála negatív oldalán van, és az FA, KE, HC szakasz hossza az A, E, ill. C ponthoz írt skálaérték abszolút értéke, vagyis FA=|x|=-x, KE=|y|=-y, HC=|z|=-z. Ezeket beírva HC=(FA+KE)/2-be, majd (-1)-gyel szorozva az állításra jutunk. ‐ Ha A és E egyike a megfelelő skála 0-pontjába kerül, vagyis x=0, ill. y=0, akkor (1)-et az AFKE trapéz helyett az AKE, ill. AFK háromszög és HC középvonala felhasználásával bizonyítjuk. Ha pedig A és E mindegyike 0-pontba, F, ill. K-ba jut, akkor C a H-ba esik, és az állítás érvényessége nyilvánvaló.
Végül, ha az FK egyenes szétválasztja az A és E pontokat, tehát x és y ellentett előjelűek, akkor az AFKE négyszög hurkolt trapéz (más szóval HC a közönséges AFEK trapézban az átlók felezőpontjainak távolsága). x és y-nak az állításban látható szimmetriája alapján feltehetjük, hogy FA≤KE, vagyis |x|≤|y|. Ha |x|=|y|, vagyis x=-y, x+y=0, akkor az AFEK négyszög paralelogramma, AE felezi FK-t, így C≡H, z=0=(x+y)/2. Ha pedig |x|<|y|, akkor C azon az oldalán van FK-nak, mint E, vagyis z előjele egyezik y-éval. Messe a Z-tengely AK-t A'-ben, FE-t E'-b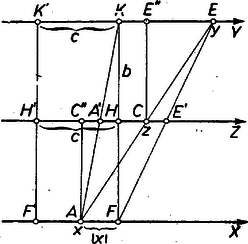en (3. ábra).
 
 
3. ábra
 

Ekkor az AFEK trapézból A'E'=(|x|+|y|)/2, az AFK és AFE háromszögekből A'H=CE'=AF/2=|x|/2, ezért
HC=A'E'-(A'H+CE')=|x|+|y|2-|x|=|y|-|x|2,
és ebből
y>0,tehátx<0,z>0eseténz=y-(-x)2=x+y2,y<0,tehátx>0,z<0esetén-z=-y-x2,


vagyis (1) ekkor is helyes. ‐ Mindezek szerint az X-, Y-, Z-skálahármas az x és y számok z számtani középértékének leolvasására alkalmas nomogram.
2. A Z-skálától a 2. részfeladatban helyébe lépő és vele egy egyenesen levő W-skála csak abban különbözik, hogy egysége feleakkora, ezért bármely szakasz mértékszáma a W-skálán 2-szer akkora, mint a Z-skálán: w=2z (ez az összefüggés negatív z és w mellett is fennáll). Innen z=w/2 és ezt (1)-be helyettesítve, majd 2-vel szorozva w=x+y (x és y előjelének bármilyen megválasztása esetén is).
Ha már most az xy¯ egyenes a W-skálát a w számmal jelölt pontban metszi, akkor az x, y, w számokkal jelölt pontok egy egyenesen vannak, tehát az xw¯ egyenes átmegy azon y számhoz tartozó ponton, amelyre w=x+y, vagyis y=w-x. Ezek szerint az X-, Y-, W-skálahármas (kéttagú) összeadásra és kivonásra alkalmas nomogram, az összeg a középső skálán olvasható le, a különbség leolvasásához pedig a kisebbítendőt a középső, a kivonandót az egyik szélső skálán keressük meg, és ekkor a különbség a másik szélső skálán adódik.
3. V-skála egysége az X- és Z-skálák egységének negyedrésze. Ha V helyén az X- és Z-vel azonos, vagyis 4-szer nagyobb egységű V' skála állna, akkor az 1. pont szerint
v'=x+z2(2)
lenne, hiszen így X, Z és V' között ugyanaz a kapcsolat állna, mint X, Y és Z között (a skálák egymástól való távolságai feleakkorák, de egymás között egyenlők). Mivel pedig v=4v', vagyis v'=v/4, ezt (2)-be helyettesítve, majd 4-gyel szorozva:
v4=x+z2,tehát valóbanv=2(x+z).(3)
4. Az U-skála egysége a V-skála egységének tízszerese, kezdőpontjuk közös (a G pont), de pozitív irányuk ellentétes. Eszerint u=-v/10, v=-10u, tehát ezt (3)-ba helyettesítve, majd -10-zel osztva, ill. rendezéssel
-10u=2(x+z),u=-x+z5,5u+x+z=0.

A 3. és 4. vizsgálatokat összefoglalva: a középső skálán (változatlan kezdőpont mellett) ahányszor kisebb (ill. nagyobb) egységet használunk, az összeget ugyanannyiszor nagyobbítva (ill. kisebbítve) kapjuk.
E skálahármasok a z=v/2-x, ill. z=-5u-x összefüggésekhez is használhatók.
5. Az Y-, Z- és T-skálák egységei és irányításuk egyezők, akárcsak az X-, Y-, Z-hármasban, de T-nek 0-pontja nem az Y- és Z-skálák 0-pontját összekötő egyenesen van, hanem attól 3 egységnyire a negatív irányban, a -3 szám ,,helyén.'' Ha tehát T helyére egy az Y-nal egyező egységű és irányítású, J- kezdőpontú T'-skálát tennénk, akkor ezen (1) szerint t'=(y+z)/2-t olvashatnánk le. Így viszont t=t'+3, vagyis t'=t-3, és ezt behelyettesítve
t-3=y+z2,t=y+z+62,2t-y-z-6=0,(4)
amit bizonyítanunk kellett. Általában, ha a számtani közép mellett egy állandó c tag szerepel, ezt a kifejezés értékének leolvasására készített nomogramban az eredményskála -c-vel való eltolásával vehetjük figyelembe.
6. Az S-skálán az Y-, Z- és T-hez képest 2-szer akkora egység szerepel, irányítása ellentétes ‐ e két tényt úgy is kimondhatjuk, hogy S egysége (-2)-szerese T egységének ‐, továbbá S kezdőpontja T-éhez képest (T egységében mérve) 8 egységgel el van tolva. Ha S helyére először a T-nek 8 egységgel való eltolásával készült S' skálát tesszük; ezen s'=t-8, ill. t=s'+8, tehát (4)-ből
2s'-y-z+10=0.
Most már S' és S kezdőpontjai közösek és s=-s'/2, s'=-2s, azért folytatólag 4s+y+z-10=0
A 2‐6. esetekben nincs szükség az előjelek vizsgálatára, mert végső soron mindegyik állítást (1)-re vezettük vissza.
 

Csákó György (Sátoraljaújhely, Kossuth L. g. II. o. t.)
 

Megjegyzések. 1. Az (1) összefüggést vegyes előjelű x és y esetére az alábbiak szerint is beláthatjuk. Toljuk el az F, K, H pontokat a maguk skáláján annak negatív irányában akkora c távolságra, hogy a kapott F', K'-höz képest A és E pozitív irányban legyenek. Ekkor C is pozitív irányban van H'-től, továbbá F'A=x+c>0, K'E=y+c>0, H'C=z+c>0, és az AF'K'E (közönséges) trapézból (3. ábra)
z+c=(x+c)+(y+c)2,és ígyz=x+y2.

2. Megkaphatjuk (1)-et így is: feltehetjük, hogy x<y. Messe az A-n át b-vel párhuzamos egyenes Z-t C''-ben és a C-n át b-vel párhuzamos az Y-t E''-ben. Ekkor C''C=z-x(>0), E''E=y-z(>0) és az ACC'', CEE'' háromszögek könnyen belátható egybevágósága alapján
C''C=E''E-bőlz-x=y-z,z=x+y2.

Mikes Endre (Budapest, Apáczai Csere J. gyak. g. II. o. t.)