Kezdőlap


Feladat:	623. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ámon Magdolna , Bede Andrea , Kóta József , Minkó Béla , Sonnevend György
Füzet:	1961/január, 16 - 18. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Mértani helyek, Síkgeometriai szerkesztések, Körök, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/február: 623. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Gondoljuk a feladatot megoldottnak és legyen $k$ középpontja $C$ , a keresett $k_{1}$ kör középpontja $C_{1}$ . Nyilvánvaló, hogy az adott $P$ -vel együtt $k_{1}$ a $k$ belsejében van, ezért a $C C_{1}$ szakasz $C_{1}$ -en túli meghosszabbításának $k_{1}$ -gyel, $k$ -val való metszéspontját $A_{1}$ -gyel, ill. $A$ -val jelölve $k_{1}$ -nek $k$ -hoz legközelebbi pontja $A_{1}$ , és a kérdéses távolság $A A_{1} = A_{1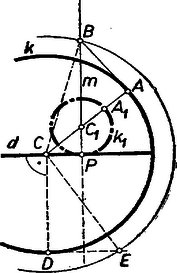} C_{1} = C_{1} P$ (1. ábra).

1. ábra

C_{1}

az érintés folytán a

d

-re

P

-ben állított

m

merőlegesen van. Húzzuk meg

k

-nak

A

-beli érintőjét, és messe ez

m

-et

B

-ben. A

B A C_{1}

és

C P C_{1}

derékszögű háromszögek hasonlók, mert

C_{1}

-nél levő szögeik csúcsszögek. Innen

\begin{matrix} B A : C P = A C_{1} : C_{1} P = (A A_{1} + A_{1} C_{1}) : C_{1} A_{1} = 2 : 1, \end{matrix}

tehát

\begin{matrix} B A = 2 C P . \end{matrix}

Ennek alapján

k_{1}

szerkesztése a következő. A

k

egy tetszés szerinti

D

pontjában húzott érintőre felmérjük a

D E = 2 C P

szakaszt;

C

körül

C E

sugárral segédkört írunk, ennek metszéspontja

m

-mel

B

;

B

-ből érintőt szerkesztünk

k

-nak ahhoz az ívéhez, amely

m

-nek

C

-vel ellentétes partján van, az érintési pont

A

;

C A

-val

m

-ből kimetsszük

C_{1}

-et;

C_{1}

körül

C_{1} P

sugárral kört írunk, ez

k_{1}

k_{1}

teljesíti a követelményt, mert egyrészt

m ⊥ d

folytán érinti

d

-t. Másrészt

C B = C E

folytán a

C A B

és

C D E

derékszögű háromszögek egybevágók, ezért

A B = D E = 2 C P

, így a két egyenlő szöggel rendelkező s így hasonló

B A C_{1}

és

C P C_{1}

derékszögű háromszögekből

\begin{matrix} A C_{1} : P C_{1} = B A : C P = 2 : 1, \end{matrix}

tehát

A C_{1} = 2 P C_{1}

és így

A A_{1} = A C_{1} - A_{1} C_{1} = 2 P C_{1} - P C_{1} = P C_{1}

.
Ha

P

különbözik

C

-től és

d

végpontjaitól, akkor a szerkesztés mindig végrehajtható és

2

megoldást ad, ezek

d

-re tükrösek. Ha ugyanis

D

-nek a

d

-re merőleges átmérő egyik végpontját választjuk, akkor

E

egyik lehetséges helyzete a

D

-nek

m

-re való tükörképe, ennélfogva

m

szétválasztja a segédkör

C

középpontját és

E

kerületi pontját, tehát metszi a segédkört.

B

-hez

A

és

A

-hoz

C_{1}

szerkesztése egyértelmű.
Eljárásunk akkor is kitűzi

A

-t, ha

P

azonos

C

-vel, de így

d ⊥ C A \equiv m

. Ekkor

C_{1}

nyilván a

d

-re merőleges sugárnak

C

-től számított első harmadoló pontja. Ha pedig

P

d

végpontja, akkor

k_{1}

ponttá fajul el, mert

P

közös pontja

k

és

k_{1}

-nek, ezért legrövidebb távolságukkal együtt a

k_{1}

kör sugara

0

Minkó Béla (Budapest, I. László g. II. o. t.)

Megjegyzés. A szerkesztés akkor is végrehajtható, ha

P

kívül van

k

-n. Az az

A

pont felel meg, amely közelebb van

m

-hez, amelyre a

C A

félegyenes metszi

m

-et.

Sonnevend György (Celldömölk, Berzsenyi D. g. II. o. t.)

II. megoldás: Használjuk tovább is az I. megoldás jelöléseit. Írjunk

C_{1}

körül

A

-n átmenő, vagyis

2

C_{1} P

sugarú

k_{2}

kört, és legyen ennek a

C_{1} P

félegyenessel közös pontja

P_{2}

(2. áb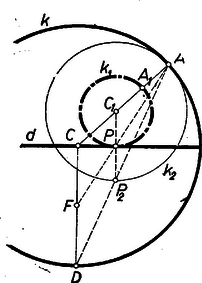ra).

2. ábra

Ekkor

P

felezi a

C_{1} P_{2}

szakaszt,

k_{2}

és

k

A

-ban érintkeznek, ezért az

A

hasonlósági centrumra nézve hasonló helyzetűek, és

P_{2}

megfelelője a

d

-re merőleges átmérőnek az a

D

végpontja, amely

d

-nek

A

-val ellentétes partján van. Így az

A C_{1} P_{2}

és

A C D

háromszögek is hasonló helyzetűek az

A

centrumra, és

P

megfelelője a

C D

sugár

F

felezőpontja.
Ennek alapján

A

-t az

F P

egyenes metszi ki

k

-ból, az a metszéspont veendő, amely a

C F

egyenes ugyanazon oldalán van, mint

P

Ámon Magdolna (Győr, Zrínyi Ilona lg. I. o. t.)

Az alábbi megoldás a következő tételen alapszik: azon pontok mértani helye, melyekre a két adott ponttól mért távolságok aránya adott,

1

-től különböző állandó: kör, az alappontokhoz és az arányszámhoz tartozó ún. Apollóniosz-kör. A tétel könnyen bizonyítható. ^{$^{*}$}

III. megoldás: Mérjük fel

m

-re

P

-től

C_{1}

irányába a

P H = C A / 2

szakaszt, a

k

kör sugarának felét (3. ábra).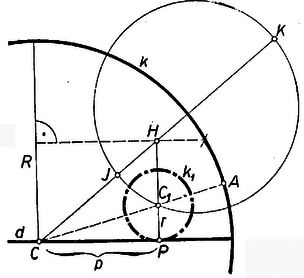

3. ábra

Ekkor

\begin{matrix} H C_{1} = H P - C_{1} P = \frac{C A}{2} - \frac{C_{1} A}{2} = \frac{C C_{1}}{2}, \end{matrix}

vagyis

H C_{1} : C C_{1} = 1 : 2

. Eszerint

C_{1}

rajta van a

H

és

C

alappontokkal és az

1 : 2

aránnyal meghatározott Apollóniosz-körön, éspedig ha a

k

belsejében levő

P

-re szorítkozunk, akkor

C_{1}

e körnek

k

belsejében levő ívén van. (Az Apollóniosz-kör egy átmérője az a

J K

szakasz, amelynek

J

végpontja a

C H

szakasznak

H

-hoz közelebbi harmadoló pontja,

K

végpontja pedig

C

-nek

H

-ra való tükörképe; ezekre ugyanis teljesül az előírt arány, másrészt a kör nyilván szimmetrikus

C H

tengelyre.)

Kóta József (Tatabánya; Árpád g. II. o. t.)

A legtöbb versenyző számítás alapján szerkesztette meg a kört. Ilyen a következő

IV. megoldás: Legyen

k

és

k_{1}

sugara

R

r

, és

C P = p (p < R)

. Ekkor a középpontok

C C_{1}

távolsága a

2 r = C_{1} A = C A - C C_{1} = R - C C_{1}

követelményből

C C_{1} = R - 2 r

. Így a

C P C_{1}

derékszögű háromszögből Püthagorász tétele alapján

\begin{matrix} {(R - 2 r)}^{2} - r^{2} - p^{2} = 3 r^{2} - 4 R r + (R^{2} - p^{2}) = 0, \end{matrix}

(1)

és innen

\begin{matrix} r = \frac{2 R \pm \sqrt[]{R^{2} + 3 p^{2}}}{3} . \end{matrix}

Mindkét gyök pozitív, mert a diszkrimináns pozitív és

4 R / 3

összegük, valamint

(R^{2} - p^{2}) / 3

szorzatuk pozitív. Számunkra csak a kisebb gyök felel meg, mert a nagyobb gyökre fennáll

\begin{matrix} r = \frac{2 R + \sqrt[]{R^{2} + 3 p^{2}}}{3} > \frac{2 R + R}{3} = R, \end{matrix}

ez pedig lehetetlen.
A kisebb gyök szerkesztése: Legyenek a

d

átmérő végpontjai

L

M

, legyen

P

tükörképe

C

-re

Q

, és a

P Q

oldalra szerkesztett szabályos háromszög harmadik csúcsa

N

. Ekkor

C N = \sqrt[]{3} p

, és így

L N^{2} = R^{2} + 3 p^{2}

, tehát

L N

-et

L

-ből

M

felé rámérve

d

-re és a végpontot

S

-sel jelölve

r

-et az

M S

szakasz harmadrésze adja.

Bede Andrea (Budapest, Szilágyi E. lg. II. o. t.)

Megjegyzések. 1. Meg lehet mutatni, hogy az (1) egyenlet nagyobb gyökével

C C_{1} = - (R - 2 r) = 2 r - R

teljesül, vagyis

C C_{1} + R = 2 r

, eszerint

k

-nak

k_{1}

-től legtávolabbi pontja van annyira

k_{1}

-től, mint

k_{1}

sugara.
2. Meg lehet mutatni, hogy a III. megoldásban adott szerkesztés a

C_{1} P

szakaszban (1) kisebb gyökét állítja elő, az Apollóniosz-körnek

m

-mel való,

k

-n kívül eső metszéspontja pedig annyira van

P

-től, mint (1)-nek nagyobb gyöke.

^{$^{*}$}Lásd pl.: Surányi János: Hasonlóság és szerkesztés, 34. o., ,,Tanulj jobban !'' könyvsorozat, Orsz. Neveléstudományi Intézet, Bpest, 1949.