Kezdőlap


Feladat:	622. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ámon Magdolna , Baróti Gy. , Benczúr A. , Dobó F. , Endreffy Z. , Farkas Z. , Felszeghy T. , Füredi G. , Gálfi László , Gáspár R. , Gyaraki K. , Görbe T. , Hargittay Á. , Jójárt I. , Kászonyi L. , Katona Éva , Katona Mária , Kerényi Ilona , Kiss Tünde , Klukovits l. , Klukovits Lajos , Konkoly K. , Kóta J. , Kucza J. , Kunszt Z. , Majoros L. , Máté A. , Máté E. , Nádasdy G. , Nováky B. , Opálény M. , Pellionisz A. , Révész M. , Schönweitz T. , Sebestyén M. (Szolnok) , Sebestyén Z. (Celldömölk) , Sonnevend Gy. , Szepesvári I. , Szidarovszky Ágnes , Szidarovszky F. , Szilágyi Mária , Tasnády Mária , Tóth Lajos (Szeged) , Tóth Vilmos , Vesztergombi Gy. , Zalán P.
Füzet:	1960/december, 209 - 213. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/február: 622. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés: A legtöbb versenyző három derékszögű háromszögre alkalmazta a Püthagorász-tételt, az így kapott egyenletrendszerből számította ki előbb a körülírt kör sugarát, majd az oldalakat, és ezek alapján végezte el a szerkesztést. A sugárra adódott másodfokú egyenletnek csak a pozitív gyökét értelmezték. Elsőnek egy ilyen megoldást mutatunk be.

I. megoldás: Legyen a háromszög köré írt

k

kör

O

középpontjának vetülete

A B

-n

D

A C

-n

E

, vagyis

O D = d

O E = e

, legyen továbbá

A B = c

A C = B C = a

és

O A = r

. Az

O A D

O A E

és

A C D

derékszögű háromszögekből ‐ feltéve, hogy

O

a háromszög belsejében van, más szóval, hogy

C

-nél hegyes szög van (1. ábra)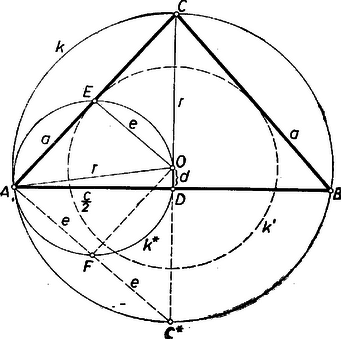

1. ábra

\begin{matrix} {(\frac{c}{2})}^{2} = r^{2} - d^{2}, & (1) \\ {(\frac{a}{2})}^{2} = r^{2} - e^{2}, & (2) \\ {(r + d)}^{2} = a^{2} - {(\frac{c}{2})}^{2}, & (3) \end{matrix}

ugyanis így a háromszögnek a tengelybe eső magassága

r + d

. Célszerű (1) és (2) alapján

a

-t és

c

-t kiküszöbölni (3)-ból:

\begin{matrix} {(r + d)}^{2} = 4 (r^{2} - e^{2}) - (r^{2} - d^{2}), \end{matrix}

rendezve

\begin{matrix} r^{2} - d r - 2 e^{2} = 0, \end{matrix}

(4)

és innen

\begin{matrix} r_{1} = \frac{d + \sqrt[]{d^{2} + 8 e^{2}}}{2} . \end{matrix}

(5)

Mivel a diszkrimináns négyzetgyökének abszolút értéke nagyobb

d

-nél, és így

\begin{matrix} r_{2} = \frac{d - \sqrt[]{d^{2} + 8 e^{2}}}{2} \end{matrix}

(6)

negatív, azért csak a pozitív

r_{1}

-et tekintjük megoldásnak.

r_{1}

alapján (1) és (2)-ből

\begin{matrix} c = \sqrt[]{8 e^{2} + 2 d \sqrt[]{d^{2} - 8 e^{2}} - 2 d^{2}}, a = \sqrt[]{4 e^{2} + 2 d \sqrt[]{d^{2} + 8 e^{2}} + 2 d^{2}}, \end{matrix}

(7)

természetesen csak a pozitív négyzetgyököt véve.

2. ábra

Ha azt tesszük fel, hogy

O

a háromszögön kívül van (2. ábra) ‐ vagyis, hogy az

A C B

szög tompaszög ‐ és

k

sugarát erre az esetre

r'

-vel jelöljük, akkor a háromszögnek a tengelybe eső magassága

r' - d

, ezért (3) így módosul:

\begin{matrix} {(r' - d)}^{2} = a^{2} - {(\frac{c}{2})}^{2} . \end{matrix}

'

)

(1) viszont nem változik meg. Célszerűbb azonban azt mondanunk, hogy

d

helyére (3)-ban és (1)-ben egyaránt

- d

lépett. Így újabb számítás nélkül a mondott változtatással átvehetjük a fenti eredményeket:

\begin{matrix} r'^{2} + d r' - 2 e^{2} = 0, & (4') \\ r'_{1} = \frac{- d + \sqrt[]{d^{2} + 8 e^{2}}}{2} és & (5') \\ r'_{2} = \frac{- d - \sqrt[]{d^{2} + 8 e^{2}}}{2} & (6') \end{matrix}

Itt csak

r'_{1}

pozitív, ezzel

c

és

a

-ra azokat a kifejezéseket kapjuk, amelyek (7)-ből

d

-nek

- d

-vel való helyettesítésével állnak elő.
Lehetséges volna az is, hogy

O

a háromszög kerületén legyen, ti. ha

d = 0

. Ebből azonnal látható, hogy

A B C

derékszögű egyenlő szárú háromszög és

a = 2 e

c = 2 \sqrt[]{2} e

, ami (7)-ből is kiadódik.
A háromszög megszerkesztése végett célszerű előbb a

k

kört előállítanunk. Ugyanis a

k

-n tetszés szerint felvett

C

csúcsból kiindulva úgy kapjuk meg a szárak egyeneseit, hogy

C

-ből érintőket húzunk az

O

körül

e

sugárral írt

k'

körhöz; ezeknek

k

-val való második metszéspontja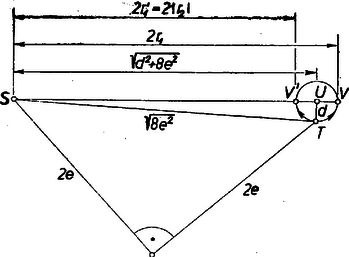

A

, ill.

B

3. ábra

k

átmérőjét (5), ill. (5

'

) alapján a következő lépésekben szerkesztjük (3. ábra).

2 e

befogókkal egyenlő szárú derékszögű háromszöget szerkesztünk, ennek

S T

átfogójára fennáll

S T^{2} = 8 e^{2}

S T

és

d

befogókkal derékszögű háromszöget szerkesztünk, ennek

S U

átfogója egyenlő az (5) és (5

'

)-beli gyökös kifejezéssel. Az

S U

egyenesre

U

-tól mindkét irányban felmérjük

d

-t, a végpontok

V

és

V'

, az utóbbi

U

-tól

S

felé. Ekkor

k

átmérője az

S V

, ill.

S V'

szakasz.
Ez a szerkesztés bármely

d

e

mellett egyértelműen végrehajtható, a fent mondott érintők szerkesztése azonban csak akkor, ha

r

nagyobbnak adódik

e

-nél. Ez (5) esetében nyilván teljesül, (5

'

)-re viszont csak akkor, ha

\begin{matrix} 2 r'_{1} = - d + \sqrt[]{d^{2} + 8 e^{2}} > 2 e, \\ d^{2} + 8 e^{2} > {(d + 2 e)}^{2} = d^{2} + 4 d e + 4 e^{2}, \\ 4 e^{2} > 4 d e, e > d . \end{matrix}

Ez a követelmény a 2. ábráról is leolvasható az

O

D

E

pontok helyzetéből. Eszerint

e > d

esetén két megoldás van,

e \leq d

esetén pedig egy.

Katona Éva(Budapest, Ybl M. ép. ip. t. II. o. t.)

Megjegyzések. 1. Vegyük észre, hogy

r_{2}

r'_{2}

abszolút értékben egyenlő

r'_{1}

-gyel, ill.

r_{1}

-gyel. Ez természetesen annak következménye, ahogyan (4

'

)-t képeztük. Mondhatjuk ugyanis azt is, hogy (4

'

) a (4)-ből úgy állt elő, hogy

r

helyére

r' = - r

-et írtunk. Ez egyben azt is jelenti, hogy elég lett volna csak pl. (4)-et felírni és ezt mondani:

d

azt jelenti, hogy mennyivel van

O

A B

oldal ,,fölött'',

r

pedig azt, hogy mennyivel van följebb

C

, mint

O

. Negatív

r

azt jelenti, hogy

C

O

alatt van (2. ábra).
2. Több dolgozatban (1) és (2) mellett az

A C D

és

O C E

háromszögek hasonlóságából adódó

\begin{matrix} \frac{c}{2} : a = e : r \end{matrix}

aránypár szerepel harmadik egyenletként. Szerzőik így látszólag megkerülték az

O

pont belső vagy külső helyzetének kérdését. Ebből az aránypár négyzetre emelésével és (1), (2) felhasználásával

r^{2}

-re kaptak másodfokú egyenletet:

\begin{matrix} (r^{2} - d^{2}) : (4 r^{2} - 4 e^{2}) = e^{2} : r^{2}, \\ r^{4} - (d^{2} + 4 e^{2}) r^{2} + 4 e^{4} = 0. & (8) \end{matrix}

Innen mind a számítás, mind a szerkesztés, mind a diszkusszió jóval bonyolultabb a fent közöltnél. Ennek az a magyarázata, hogy (8) bal oldalában (4) és (4

'

) bal oldalának szorzata áll előttünk, ugyanis

\begin{matrix} r^{4} - 4 e^{2} r^{2} + 4 e^{4} - d^{2} r^{2} = {(r^{2} - 2 e^{2})}^{2} - d^{2} r^{2} = (r^{2} - 2 e^{2} - d r) (r^{2} - 2 e^{2} + d r) . \end{matrix}

(8)-ból

r^{2}

-re két pozitív gyököt kapunk, mert mind a diszkrimináns:

\begin{matrix} {(d^{2} + 4 e^{2})}^{2} - 16 e^{4} = d^{2} (d^{2} + 8 e^{2}), \end{matrix}

mind a gyökök szorzata:

4 e^{4}

, mind összegük:

d^{2} + 4 e^{2}

pozitív. Ezekből négyzetgyökvonás útján kapjuk azt a két egyenlő abszolút értékű, ellentett előjelű gyökpárt, amelynek elemei fent külön választva adódtak.

II. megoldás: Legyen ‐ az I. megoldás jelöléseivel ‐ a

k

körön a

C

-vel átellenes pont

C^{*}

, és

O

vetülete

A C^{*}

-on

F

(1. és 2. ábra). Thalész tétele szerint

A C^{*} ⊥ A C

, így az

A E O F

négyszög téglalap, köréje kör írható. E

k^{*}

kör középpontja az

O A

szakasz felezőpontja, ezért

k^{*}

átmegy a

D

talpponton is. Továbbá

F

felezi

A C^{*}

-ot, így

C^{*} F = F A = O E = e

és

C^{*} A = 2 e

.
Alkalmazzuk a körhöz külső pontból húzható szelők metszeteire vonatkozó tételt

k^{*}

-ra és

C^{*}

-ra

\begin{matrix} C^{*} O \cdot C^{*} D = C^{*} F \cdot C^{*} A, \end{matrix}

vagyis az 1., ill. a 2. ábra eseteiben

\begin{matrix} r (r - d) = e \cdot 2 e = 2 e^{2}, ill. r (r + d) = 2 e^{2} . \end{matrix}

(9)

Ezzel megkaptuk az I. megoldás (4), ill. (4

'

) egyenletét. Tovább ismét az I. megoldás szerint haladhatunk.

Gálfi László (Budapest, Fazekas M. gyak. gimn. II. o. t.)

Megjegyzések. 1. A 3. ábrát felére kicsinyítve (vagyis a befogókat

e

e

, majd

d / 2

-nek véve) a szerkesztést úgyis értelmezhetjük, mint a (9) egyenlet szerkesztéssel való olyan megoldását, amely a legutóbb idézett tételt használja fel. A (9) bal oldalán álló tényezők különbsége ismert szakasz:

d

, az egyik tényező pedig éppen az ismeretlen. Ezért olyan kört veszünk, melynek átmérője

d

, egyik szelőként pedig majd a külső pontot a középponttal összekötő egyenest. A külső pont helyzetét a jobb oldal alapján tűzzük ki: úgy, hogy a belőle húzott érintő egyenlő legyen a jobb oldali tényezők mértani középarányosával.

Klukovits Lajos (Szeged, Radnóti M. g. I. o. t.)

2. Az 1. megjegyzés gondolatát folytatva

e < d

esetén

r

a következőképpen is szerkeszthető. Legyenek

L

M

N

egy egyenes olyan pontjai, amelyekre

L M = M N = e

, az

M N

alap fölé

d / 2

szárral szerkesztett egyenlő szárú háromszög harmadik csúcsa

O

, és messe az

O L

egyenest az

O

körül

d / 2

sugárral írt kör

P

és

P'

-ben. Ekkor

r

értéke

L P

, ill.

L P'

.
3. Egy tetszés szerinti háromszög szögei legyenek

α

β

γ

, a körülírt kör

O

középpontjának e szögekkel szemközti oldalaktól mért távolsága rendre

d

e

f

(4. á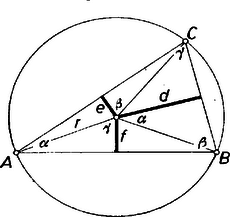bra).

4. ábra

A középponti és kerületi szögekre vonatkozó összefüggésekből következik, hogy az

O

-ból az oldalakra bocsátott merőlegesek az oldal végpontjaihoz húzott sugarakkal rendre

α

β

γ

nagyságú szögeket zárnak be. Így

\begin{matrix} cos α = \frac{d}{r}, cos β = \frac{e}{r}, cos γ = \frac{f}{r} . \end{matrix}

Ez tompaszögű háromszögre is érvényes, ha abban az esetben, amikor az

O

pont és a háromszög valamelyik oldalnak ellenkező oldalára esnek, akkor az oldaltól mért távolságot negatívnak vesszük. Másrészt az

α + β + γ = 180^{\circ}

összefüggés folytán

\begin{matrix} cos^{2} α & = cos^{2} [180^{\circ} - (β + γ)] = {[- cos (β + γ)]}^{2} = \\ = cos^{2} β cos^{2} γ + sin^{2} β sin^{2} γ - 2 cos β cos γ sin β sin γ = \\ = cos^{2} β cos^{2} γ + (1 - cos^{2} β) (1 - cos^{2} γ) - 2 cos β cos γ sin β sin γ = \\ = 1 - cos^{2} β - cos^{2} γ + 2 cos β cos γ (cos β cos γ - sin β sin γ) = \\ = 1 - cos^{2} β - cos^{2} γ + 2 cos β cos γ (β + γ) . \end{matrix}

Innen

\begin{matrix} 1 - cos^{2} α + cos^{2} β - cos^{2} γ - 2 cos α cos β cos γ = 0, \end{matrix}

és ha

β = γ

, akkor a bal oldal szorzattá alakítható:

\begin{matrix} 1 - cos^{2} α - 2 cos^{2} β - 2 cos α cos^{2} β = (1 + cos α) (1 - cos α - 2 cos^{2} β) . \end{matrix}

Valódi háromszög esetén

α < 180^{\circ}

, s így

1 + cos α \neq 0

, tehát egyenlő szárú háromszögben, ha

α

a szárak közti szög,

\begin{matrix} 1 - cos α - 2 cos^{2} β = 0. \end{matrix}

Beírva a koszinuszok kifejezését

d

e

f

r

segítségével és a törteket eltávolítva tetszés szerinti háromszögre

\begin{matrix} r^{3} - (d^{2} + e^{2} + f^{2}) r - 2 d e f = 0, \end{matrix}

egyenlő szárú háromszögre pedig

\begin{matrix} r^{2} - d r - 2 e^{2} = 0 \end{matrix}

kell, hogy teljesüljön. Az utóbbi a fenti megoldásokban is szereplő egyenlet, az előbbi alapján pedig belátható, hogy általános háromszög esetén a kitűzött feladat megfelelője általában nem oldható meg a szokásos ún. eukleidészi körző-vonalzós szerkesztések segítségével.¹
A körzővel és vonalzóval végrehajtható szerkesztésekre vonatkozóan lásd lapunk egy korábbi cikkét: Surányi János: A szögharmadolás kérdéséről, Középisk. Matematikai Lapok XIV. (1957), 97‐107. és 129‐134. o.

¹Lásd Szőkefalvi Nagy Gyula: Zwei nichtkonstruierbare Aufgaben des Dreiecks. Elemente der Mathematik, 6 (1951), 81‐83. o.