Feladat: 619. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Horváth Kálmán ,  Kiss Tünde ,  Schőnweitz Tivadar ,  Szepesvári István ,  Vesztergombi György 
Füzet: 1960/december, 205 - 207. oldal  PDF  |  MathML 
Témakör(ök): Algebrai átalakítások, Másodfokú diofantikus egyenletek, Gyakorlat
Hivatkozás(ok):Feladatok: 1960/február: 619. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Egyenletünk x és y-ra szimmetrikus, másodfokú, határozatlan egyenlet, a megoldásra vonatkozó Diophantosz-i követelménnyel. Tekintsük benne egyedül x-et ismeretlennek, y-t pedig olyan paraméternek, amely csak egész értékeket vehet fel. 0-ra redukálva, majd az oldóképlettel:

x2-(y+1)x+(y2-y)=0,x=y+1±(y+1)2-4(y2-y)2(2)


x akkor és csak akkor valós, ha a D diszkrimináns nem negatív, akkor és csak akkor racionális, ha D teljes négyzet, végül akkor és csak akkor egész, ha (2)-ben a számláló páros. D=0 áll be, ha
(y+1)2-4(y2-y)=-3y2+6y+1=0,
vagyis
y'=-6+48-6≈-0,15...ésyn=-6-48-6≈2,15...
Ezekkel a másodfokú egyenlet gyöktényezős alakja alapján D így írható:
D=-3(y-y')(y-y'').(3)
Eszerint, az y'<y'' nagyságviszonyra tekintettel, D>0 csak a
y'<y<y'',azaz-0,15...<y<2,15...(4)
értékekre teljesül, mert a (3)-beli különbségek csak így ellentett jelűek. (4)-nek a következő három egész szám tesz eleget:
y1=0,y2=1,y3=2.
Velük D mindegyik esetben teljes négyzet: 1, 4, 1, és négyzetgyöke ellentétes párosságú y-nal, ennélfogva egyező párosságú (2) számlálójának első tagjával, y+1-gyel, így x mindig egész:
x11=0,x21=0,x31=1,x12=1;x22=2,x32=2.

Mindezek szerint egyenletünk megoldásai a következő számpárok:
(0,0),(1,0),(2,1),(2,2),(1,2)és(0,1).

Horváth Kálmán (Kaposvár, Táncsics M. g. II. o. t.)
 

Megjegyzések. 1. D nem negatív voltának és teljes négyzet voltának előírását egybe kapcsolhatjuk a D=e2 követelménybe, ahol e nemnegatív egész szám. Ekkor
-3y2+6y+1=e2,y=3±12-3e23=1±4-e23,
és mivel y is egész, azért (4-e2)/3=f2, ahol nem negatív egész, másképpen e2+3f2=4. Ezt nyilván csak e2=f2=1 és e2=4, f2=0 elégíti ki, és ezekből jutunk az y=0 és y=2, valamint y=1 értékekre.
 

Schönweitz Tivadar (Pannonhalma, Bencés g. II. o. t.)
 

2. Burkoltabb formában, de lényegében ugyanerre jut a következő megoldás is.
Legyen x+y=u és x-y=v, és fejezzük ki 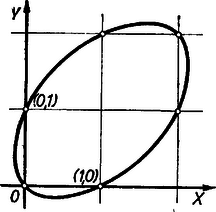x2+y2-t és xy-t az
(x2+y2)+2xy=u2(x2+y2)-2xy=v2
egyenletrendszerből: x2+y2=(u2+v2)/2, xy=(u2-v2)/4. Ezeket (1)-be helyettesítve
4u=u2+3v2,másképpen(u-2)2+3v2=4,
amiből I: u-2=±2 és v=0, ez u, v-re 2 megoldás, továbbá II: u-2=±1, v=±1, további 4 megoldás. Minden egyes u, v megoldásból egy x, y megoldást kapunk a helyettesítést visszafordító x=(u+v)/2, y=(u-v)/2 képletekből, és ezek egészek, mert a kapott u, v értékpárok tagjai egyenlő párosságúak.
 
 

3. Bizonyítás nélkül megjegyezzük, hogy az adott egyenlet 0-ra redukált alakjának a koordináta-rendszerben az ábrán látható ellipszis felel meg. Látjuk, hogy a vonal csak a kapott 6 rácsponton megy át, vagyis csak e 6 pontjának mindkét koordinátája egész szám. (Olyan pontja nincs is az ellipszisnek, amelyre csak az egyik koordináta egész.)
 

II. megoldás: Az (1) egyenlet x és y-ra szimmetrikus, másodfokú, ezért bármelyik ismeretlen értékét megválasztva a másikra legfeljebb 2 érték adódik. Könnyű látni, hogy az I: x=y=0 értékpár kielégíti az egyenletet. Keressük meg az y=0 mellett adódó második x gyököt! Ekkor (1) így alakul: x=x2, ennek egyik gyöke x1=0, amit újra meg kellett kapnunk, a másik x2=1, egész szám. Kaptuk a II: (1,0) értékpárt. Ebből x és y felcserélésével kapjuk a III: (0,1) értékpárt. Eszerint y=1 mellett is van megoldás, keressük meg ismét a másik x-et: x+1=x2-x+1-ből x1=0 (ez a III) és x2=2, egész szám, tehát IV: (2,1). Ebből felcseréléssel V:(1,2) és y=2-ből kiindulva hasonlóan VI: (2,2).
Ezek után meg kell mutatnunk, hogy több megoldás nincs. Minden más megoldásban x és y vagy 0-nál kisebb, vagy 2-nél nagyobb egész szám volna.
Könnyű belátni, hogy x, y mindegyike nem lehet negatív, mert (1)-ből átrendezéssel
x+y-xy=(x-y)2,
és itt x<0, y<0 mellett a bal oldal negatív, a jobb oldal pedig 0, vagy pozitív. Ugyanezért olyan megoldás sincs, amelyben x és y nagyobb 2-nél; az ellenkező esetben ugyanis volna olyan pozitív s, t számpár, amelyre x=2+s, y=2+t, és teljesülne az (1)-ből adódó
(2+s)+(2+t)=(2+s)2-(2+s)(2+t)+(2+t)2,
másképpen
-(s+t+st)=(s-t)2
egyenlet. Végül hasonlóan olyan megoldás sincs, melyben x, y egyike negatív másika nagyobb 2-nél, pl. x<0 és y=2+t, ahol t>0, mert ezekkel (1)-ből,
3x-3t+xt=x2+t2+2,
és itt a bal oldal negatív volna, a jobb oldal pedig pozitív.
Ezzel a megoldást befejeztük.
Összeállítva a következők dolgozatából:
Szepesvári István (Budapest, Apáczai Csere J. gyak. g. II. o. t.)
Vesztergombi György (Budapest, Piarista g. II. o. t.)

 

Megjegyzés. Az utolsó átalakítás helyett az alábbiak szerint is beláthatjuk, hogy lehetetlenségre vezet x<0, y>2 alakú megoldás feltételezése. (1) átalakításával
(x2-x)+(y2-y)=xy,másképpenx-1y+y-1x=1,
és itt a bal oldal mindkét tagja negatív vagy 0 lenne.
 

Kiss Tünde (Tamási, Béri Balogh Á. g. II. o. t.)
 

III. megoldás: Az egyenlet jobb és bal oldalának különbségét 2-vel szorozva a kifejezést négyzetekké tudjuk alakítani:
2x2-2xy+2y2-2x-2y=x2-2xy+y2+x2-2x+y2-2y==(x-y)2+(x-1)2+(y-1)2-2.
Egyenletünk tehát a következő alakban írható:
(x-y)2+(x-1)2+(y-1)2=2.
Ez egész x, y értékekre csak úgy teljesülhet, ha két négyzet értéke 1, a harmadiké 0. A lehetséges megoldások tehát:
 

a) x=y,  x-1=±1(=y-1), azaz  x=y=0  vagy  x=y=2;b)x=1,  x-y=±1, azaz  y=0,2; és ekkor  y-1=±1  is teljesül;c)y=1,  x-y=±1, azaz  x=2,0, (ekkor  x-1=±1).