Feladat: 614. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Benczúr A. ,  Csákó Gy. ,  Endreffy Z. ,  Farkas Z. ,  Felszeghy T. ,  Gálfi l. ,  Gáspár R. ,  Katona Éva ,  Kunszt Z. ,  Minkó B. ,  Nádasdy G. ,  Nagy Dénes L. ,  Nováky B. ,  Sebestyén Z. ,  Szepesvári I. ,  Szidarovszky Ágnes ,  Szidarovszky F. ,  Zalán Péter 
Füzet: 1960/november, 154 - 156. oldal  PDF  |  MathML 
Témakör(ök): Terület, felszín, Trapézok, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1960/január: 614. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az ABCD trapéz ismeretlen párhuzamos oldalai AB=a és CD=c, adott szárai BC=b és DA=d, adott átlói 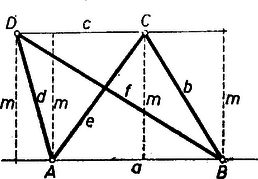AC=e, BD=f.

 
 

Az oldalak párhuzamossága egyenlőség alakjában azzal jellemezhető, hogy az ABC és ABD háromszögpárban a közös a alaphoz tartozó magasságok egyenlők. Ebből továbbmenve a területek is egyenlők. Ezt a Heron-képlettel kifejezve ‐ annak beszorzással előálló
16t2=2(a2b2+b2c2+c2a2)-(a4+b4+c4)
alakjából, ahol a, b, c az oldalak ‐ egyismeretlenes egyenletet kapunk a-ra (pontosabban: elsőfokú egyismeretlenes egyenletet a2-re):
16t2=2(a2b2+b2e2+e2a2)-(a4+b4+e4)=2(a2f2+f2d2+d2a2)-(a4+f4+d4).


Innen
a2=(b4-2b2e2+e4)-(f4-2f2d2+d4)2(b2+e2-f2-d2)=(e2-b2)2-(f2-d2)22(b2+e2-f2-d2),a2=(e2+f2-b2-d2)(e2+d2-b2-f2)2(e2+b2-f2-d2).(1)



Ugyanezzel a meggondolással fejezhető ki c2 az ACD és BCD háromszögek területének egyenlőségéből. Ekkor mindössze c=CD és a=AB szerepe cserélődik meg, c2 keresett kifejezését tehát megkapjuk, ha A és D szerepét és egyidejűleg B és C-ét felcseréljük. Így
b=BChelyéreCB=blép,d=AD,,DA=d,,e=AC,,DB=f,,f=BD,,CA=e,,
tehát csak e és f cserélődik meg:
c2=(f2+e2-b2-d2)(f2+d2-b2-e2)2(f2+b2-e2-d2)(2)
Vegyük észre, hogy (2) számlálójának 2-ik tényezője és nevezőjének betűs tényezője úgy is előáll, ha (1) megfelelő tényezőit felcseréljük, majd (-1)-gyel szorozzuk. Ez az észrevétel megkönnyíti a számítást. A két (-1)-gyel való szorzás természetesen el is maradhat. (Ugyanezen eredményre jutottunk volna az A, C és B, D betű-párok tagjainak kölcsönös felcserélésével is.)
A számításokban a két szár-adatot nyilván tetszés szerint oszthatjuk el b és d szerepére. Ez után e és f megválasztására 2 lehetőség látszik, de az egyikről a másikra való áttérés ‐ vagyis e és f cseréje ‐ mint láttuk ‐ csupán felcseréli a-t c-vel.
A számpéldákban
I. b=60, d=61, e=100, f=109-el a=80 és c=91; ez a trapéz derékszögű, BC⊥AB.
II. b=60, d=109, e=61, f=100-zal a=11 és c=80. Ez a trapéz hurkolt, a B csúcsnál az ABC háromszögben kisebb szög adódik, mint ABD-ben.
III. b=d=25, e=f=50-nel a és c kifejezése határozatlan, 0/0 alakú.
IV. b=d=17, e=25, f=39-cel a=c=28, ez a trapéz egyszersmind paralelogramma, mert párhuzamos oldalai egyenlők.
A III. példában mind a szárak, mind az átlók egyenlők, ezért a trapéz szimmetrikus. A határozatlanság magyarázata, hogy két adat: szár és átló nem határozza meg egyértelműen a szimmetrikus trapézt. Az ABC és ABD háromszögek mindegyikéből a háromszög-egyenlőtlenséggel 25<a<75 adódik, e korlátok között választott bármely a-val az ABC és BAD háromszögek tükrösek AB felező merőlegesére, és így CD párhuzamos AB-vel.
A IV. példa is egyenlő szárú, de különböző átlójú trapéz. Ilyen minden ferdeszögű paralelogramma.
 

Zalán Péter (Aszód, Petőfi S. g. II. o. t.)
 

Megjegyzés. Az (1) és (2) eredmények teljes diszkusszióját mellőzve csak a következőkre mutatunk rá:
1. a háromszög-egyenlőtlenséget az átlók e1, e2, f1, f2 metszetei és a b, d szár által meghatározott két háromszögre alkalmazva, majd összeadással kapjuk, hogy konvex trapézban egyrészt (e1-f1)+(e2-f2)=e-f<b+d, másrészt (e1+f1)+(e2+f2)=e+f>b+d.
2. b=d és e≠f esetén a=c, a négyszög paralelogramma.
3. e=f és b≠d esetén a=c, a négyszög hurkolt, csúcsait az a, c oldalakkal és b, d átlókkal bíró paralelogramma csúcsai adják. (A 2. megállapítás szemléletesen is belátható: az AB és CD párhuzamos egyenesek távolságának bármely alkalmas ‐ b, d, e, f mindegyikénél kisebb ‐ megválasztása esetén az egyenlő b, d szakaszpár egymáshoz képest kétféleképpen illeszthető AB és CD közé; ha nem párhuzamosak, akkor végpontjaik szimmetrikus trapézt alkotnak, de ezt e≠f kizárja; tehát párhuzamosak. Hasonlóan látható be a 3. is.)
4. Nincs megoldás, ha a és c nevezője 0. Ilyenkor e>d esetén e2-d2=f2-b2=g2(>0), eszerint van olyan konvex trapéz, melynek magassága és egyik szára g, párhuzamos oldalai b és d, átlói e és f, és olyan konvex trapéz is, melyben g átló, e és f szárak.