Kezdőlap


Feladat:	613. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benczúr A. , Dóra L. , Dringó L. , Endreffy Z. , Fajszi Csaba , Farkas Z. , Földes I. , Gálfi l. , Gáspár R. , Góth L. , Gyaraki K. , Katona Mária , Kender Etelka , Kerényi Ilona , Kéry G. , Kiss G. , Kóta J. , Kunszt Z. , Lehel J. , Nováky B. , Opálény Mihály , Raffay I. , Sebestyén Z. , Simonovits Miklós , Sonnevend Gy. , Szepesvári I. , Szidarovszky F. , Tasnády Mária , Tekulics P. , Tóth Klára , Vesztergombi Gy. , Visy Zs. , Zalán P. , Zsiday-Galgóczy K.
Füzet:	1960/november, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Pont körüli forgatás, Szögfelező egyenes, Körülírt kör, Hozzáírt körök, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1960/január: 613. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Gondoljuk a feladatot megoldottnak és a nyert $A B C$ háromszög $B A C$ szöge, $A A'$ szögfelezője és kerülete legyen egyenlő rendre az adott $α$ szöggel, ill. az $f$ , $2 s$ szakasszal. Rajzoljuk meg a háromszög oldalegyeneseinek azt a $k$ érintő körét (1. ábra), amely a $B C$ oldalt kívülről érinti, és legyen ennek középpontja $O$ , érintési pontja az $A B$ , $B C$ , $C A$ oldalon rendre $K$ , $L$ , $M$ (közülük $L$ a $B C$ szakaszon, $K$ és $M$ az oldalak $B$ -n, $C$ -n túli meghosszabbításán).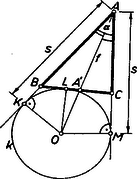

1. ábra

Ekkor

O

A A'

egyenesen van, a

B

-ből,

C

-ből, majd

A

-ból húzott érintőszakaszok egyenlők:

B K = B L

C L = C M

A M = A K

, és így

A K = (A K + M A) / 2 = (A B + B K + M C + C A) / 2 = (A B + B L + L C + C A) / 2 = s

.
Ezek alapján a szerkesztés a következő: az

α

szög száraira felmérjük az

A K = A M = s

szakaszt, a

K

és

M

-ben a szárakra emelt merőlegesek

O

metszéspontja körül

O K

sugárral megszerkesztjük

k

-t, az

A O

-félegyenesre felmérjük

A A' = f

-et és a nyert

A'

-ből

k

-hoz húzott érintővel a száraiból kimetsszük

B

C

-t.
A kapott

A B C

háromszög megfelel a követelményeknek, mert

B A C ∢ = α

A A'

felezi e szöget és

A'

-ben lép ki a

B C

oldalon, és

A B + B C + C A = A B +

+ B L + L C + C A = (A B + B K) + (M C + C A) = 2 s

.
A megoldások száma 2, 1, 0 aszerint, hogy

A'

k

-hoz képest külső, ill. kerületi, ill. belső pont (vagy

f > O A

), és így az

A'

-ből 2. 1, ill. 0 (az

A

-t és

O

-t szétválasztó) érintőt lehet húzni. Ha 2 megoldás adódik, ezek

A O

-ra tükrösek, ha pedig 1 adódik, akkor a háromszög egyenlő szárú.

Opálény Mihály (Budapest, Piarista g. II. o. t.)

Megjegyzés. Trigonometriai ismeretekre támaszkodva a megoldhatóság

A A' \leq A O - O K

feltételét így is írhatjuk:

\begin{matrix} f \leq \frac{s}{cos \frac{α}{2}} - s tg \frac{α}{2} = \frac{s (1 - sin \frac{α}{2})}{cos \frac{α}{2}} . \end{matrix}

Kender Etelka (Tata, Eötvös J. g. II. o. t.)

II. megoldás: Legyen az

A

csúcs tükörképe a háromszög

B

-nél,

C

-nél levő külső szögének felezőjére

A_{1}

, ill.

A_{2}

(2. 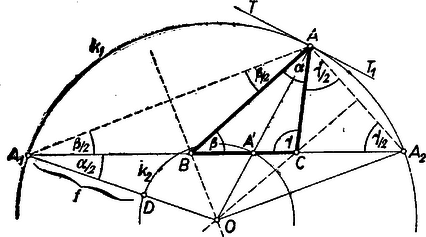ábra).

2. ábra

Így az

A B A_{1}

és

A C A_{2}

háromszögek egyenlő szárúak,

A

-nál levő szögük a külső szög tétele szerint fele az

A B C = β

, ill. A

C B = γ

szögnek, ugyanis

A_{1}

A_{2}

B C

oldal meghosszabbításaira esnek, tehát

\begin{matrix} A_{1} A A_{2} ∢ = \frac{β}{2} + α + \frac{γ}{2} = 90^{\circ} + \frac{α}{2} . \end{matrix}

Továbbá

\begin{matrix} A_{1} A_{2} = A_{1} B + B C + C A_{2} = A B + B C + C A = 2 s . \end{matrix}

A használt tükrös tengelyek metszéspontját

O

-val jelölve

O A_{1} = O A_{2} = O A

, tehát

O

A A_{1} A_{2}

háromszög

k_{1}

körülírt körének középpontja. Másrészt szerkesztésénél fogva

O

A B C

háromszög oldalait érintő körök közül a

B C

oldalt kívülről érintő körnek középpontja, tehát

O A

felezi a

B A C = α

szöget, ezért

O A_{1} B ∢ = O A B ∢ = α / 2

.
Ezek alapján az

O A_{1} A_{2}

egyenlő szárú háromszög a

2 s

alapból és a rajta fekvő

α / 2

(hegyes) szögből megszerkeszthető és folytatólag megrajzolhatjuk

k_{1}

-et. Másrészt

O A_{1}

-re

A_{1}

-től

A_{1} D = A A' = f

-et felmérve az

O D

szakaszban megkapjuk

O A - A A' = O A'

-t, és az

O

körül

O D

sugárral írt

k_{2}

körrel

A_{1} A_{2}

-ből kimetszhetjük

A'

-t. Ezután az

O A'

félegyenessel

k_{1}

-ből kimetsszük

A

-t, végül

A A_{1}

és

A A_{2}

felező merőlegesével

A_{1} A_{2}

-ből kimetsszük

B

-t,

C

-t.
A megoldhatóság feltétele, hogy

O D = O A_{1} - f

nagyobb legyen

O

-nak

A_{1} A_{2}

-től való távolságánál.

Fajszi Csaba (Budapest, Rákóczi F. g. II. o. t.)

Megjegyzés. Ha

A_{1}

A_{2}

-t

A

-nak

B

, ill.

C

körül

B C

meghosszabbításaira való ráforgatásával állítottuk elő,

k_{1}

-et pedig az

A A_{1} A_{2}

háromszög körülírt körének tekintjük, akkor a következő meggondolással láthatjuk be, hogy

A O

felezi a

B A C = α

szöget. Húzzuk meg

k_{1}

-nek

A

-beli

T T_{1}

érintőjét. Ekkor a kerületi szögek tétele szerint

T A A_{1} ∢ = A A_{2} A_{1} ∢ = γ / 2

, tehát

\begin{matrix} O A B ∢ = O A T ∢ - T A A_{1} ∢ - A_{1} A B ∢ = 90^{\circ} - γ / 2 - β / 2 = α / 2. \end{matrix}

Kerényi Ilona (Debrecen, Kossuth L. gyak. g. II. o. t.)

III. megoldás: Legyen

A'

vetülete az

A B

A C

egyenesre

P

Q

, és forgassuk el az

A' B P

derékszögű háromszöget

A'

körül úgy, hogy

P

csúcsa

Q

-ba essék, legyen

B

új helyzete a

C A

félegyenesen

B_{1}

(3. áb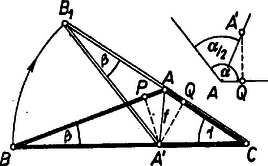ra).

3. ábra

Ekkor az

A' B_{1} C

háromszög hasonló

A B C

-hez (körüljárásuk ellentétes irányú), mert

C

szögük közös,

B

, ill.

B_{1}

-nél levő szögük egyenlő. Így

A' C B_{1}

-ből ismerjük

A'

-nél levő szögét,

A' Q

magasságát (megkaphatjuk egy az

A A' Q

derékszögű háromszöggel egybevágó háromszögből, melyben az átfogó

f

és egyik hegyes szög

α / 2

), végül a kerületét.
Ugyanis

\begin{matrix} C A' + A' B_{1} + B_{1} C = C A' + A' B + B_{1} Q + Q C = C B + B P + Q C = \\ = C B + (B A - P A) + (A C - A Q) = 2 s - 2 A Q, \end{matrix}

ahol

A Q

a fenti derékszögű háromszög másik befogója. (

+ Q C

helyett

- Q C

áll, ha

γ > 90^{\circ}

, de a végeredmény ugyanaz.) Ennélfogva az

A' B_{1} C

háromszög megszerkeszthető.
Ha ugyanis

A'

-t

B_{1}

és

C

körül

B_{1} C

meghosszabbításaiba forgatjuk és új helyzetei

A_{1}'

A_{2}'

, akkor

A_{1}' A'_{2} = 2 s - 2 A Q

és

A_{1}' A' A'_{2} ∢ = 90^{\circ} + α / 2

, tehát

A'

mértani helye egyrészt a látószögkörív, másrészt az

A_{1}' A_{2}'

-től

A' Q

távolságban haladó párhuzamos. (Az ábra hasonlóságokat mutat a 2. ábrához, ezért mellőzzük.)

A' B_{1} C

-ből az

A' B_{1} Q

háromszög

A'

körüli ,,visszaforgatásával'' kaphatjuk

B

és

P

-t (

B

C A'

félegyenesen,

A'

-n túl) és

B P

kimetszi

C B_{1}

-ből

A

-t.

Simonovits Miklós (Budapest, Radnóti M. g. II. o. t.)