Feladat: 612. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: nehéz
Megoldó(k):  Nádasdy G. ,  Palánkai Gellért 
Füzet: 1960/november, 150 - 152. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Numerikus és grafikus módszerek, Hossz, kerület, Gyakorlat
Hivatkozás(ok):Feladatok: 1960/január: 612. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Vegyünk fel egy derékszöget, rajzoljuk meg a szárait érintő, 50 mm sugarú kört, ennek azt az érintőjét, amely a szárakhoz 45∘ szöggel hajlik és amelynek a kör ugyanazon oldalán van, mint a derékszög csúcsa. Körünk a létrejött derékszögű egyenlő szárú háromszögnek beírt köre, kerülete k=100π≈ ≈314 mm. A háromszög oldalait 0,5 mm pontossággal 170,5, 170,5 és 241,5 mm-nek találjuk, így kerülete k1=582,5 mm, nem éri el 2k-t. (k1 indexében ‐ és később a szögekében is ‐ a próbálkozás sorszámára utalunk.)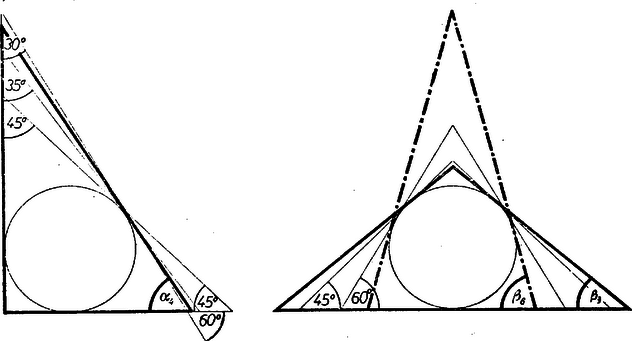
Tartsuk állandónak a derékszöget és a kört, és próbálkozzunk más érintőkkel. Ezek helyzetét az előálló derékszögű háromszög nagyobb α hegyes szögével adjuk meg. Legyen α2=60∘, így a kerület: k2≈136,5+236,5+273,0=646,0 mm, nagyobb 2k-nál.
Fogadjuk el bizonyítás nélkül hogy α növelésével a fentihez hasonlóan szerkesztett derékszögű háromszög kerülete egyre nagyobbnak adódik. Ez valószínű, ugyanis így csak a kisebb befogó válik kisebbé, és ez is mindig nagyobb marad a kör átmérőjénél, a nagyobb befogó viszont akármilyen naggyá lehet, az átfogó pedig még ennél is nagyobb. Eszerint 45∘-ról 60∘-ra áttérve már túlmentünk a kívánt tulajdonságú a szögön. ‐ k1 hiánya 2k-hoz képest 628,0-582,5=45,5 mm, k2 többlete pedig 646,0-628,0=18,0 mm, kisebb a hiánynál. Ez arra mutat, hogy α-t 60∘-hoz közelebb keressük.
α3≈55∘-kal k3≈146,0+208,5+254,5=609,0 mm, hiánya 2k-hoz képest 19,0 mm. k2 és k3 alapján úgy látszik, hogy 57∘, vagy 58∘ lesz a keresett szög.
α4≈58∘-kal k4≈140,0+224,5+264,5=629,0 mm, α5≈57∘-kal pedig k5≈142,0+219,0+261,0=622,0 mm, ezek közrefogják 2k-t, a k4-2k eltérés 1,0 mm, a 2k-k5 eltérés pedig 6,0 mm.
Ezek szerint a kívánt tulajdonságú derékszögű háromszög hegyes szögei 58∘ és 32∘.

 
 

II. Az előírt tulajdonságú egyenlő szárú háromszöget keresve tartsuk ismét állandónak az alap egyenesét, és a beírt kört. Így a háromszögek tengelye is állandó, és elég a szár és az alap fele hosszát mérnünk, ennek k-val kell egyenlőnek lennie. A szár irányát az alappal bezárt β szögével adjuk meg, a megvizsgált háromszögek ezen szögét és félkerületét rendre β1,β2,...,s1,s2,...-vel jelöljük.
Induljunk ki a szabályos háromszögből, tehát legyen β1≈60∘, így s1≈ ≈173,0+86,5=219,5 mm, kisebb k-nál. Hallottuk, hogy az ugyanakkora kerületű háromszögekbe írt körök közül a szabályos háromszögbe írt kör sugara a legnagyobb; valószínű ebből, hogy fordítva ugyanazon kör köré írt háromszögek közül a szabályos háromszög kerülete a legkisebb. Eszerint β növelésével és csökkentésével egyaránt várható a háromszög kerületének növekedése, mert a nagyon ,,magas'' és nagyon ,,lapos'' háromszögek kerülete egyaránt nagyobb a szabályos háromszögénél. Mindkét irányban csak egy-egy megoldás várható.
β2≈45∘ esetére előbbi vizsgálatunkból s2=k1/2≈291,0 mm, ez valóban nagyobb s1-nél, de még kisebb k-nál. β3≈40∘ mellett s3≈179,5+137,0=316,5 mm, ez már kissé sok, β4≈41∘ mellett viszont s4≈177,0+133,5=310,5 mm hiányt mutat, és a k-s4≈3,5 mm hiány nagyobb az s3-k≈2,5 mm többletnél. Így β≈40∘-kal megfelelő háromszöget kaptunk, szögei 40∘, 40∘, 100∘.
Másrészt β5≈70∘-kal s5≈209,0+71,5=280,5 mm, ami kevés, a k-s1≈94,5 mm hiány k-s5≈33,5 mm-re, közel harmadára csökkent, ezért β-t az előbbi β5-β1=10∘-nál kevesebbel növeljük. β6≈75∘-kal s6≈251,5+65,0=316,5 mm, kissé sok, de már β7≈74∘-kal s7≈240,5+66,5=307,0 kevés. A k-tól való eltérés s6-nál kisebb, így a második megfelelő háromszög szögei 75∘, 75∘, 30∘.
 

Palánkai Gellért (Szeged, Radnóti M. g. I. o. t.)
 

Megjegyzések. 1. Kevesebb méréssel érünk célt az I. részben, ha figyelembe vesszük, hogy a háromszög kerülete a csúcsokból a körhöz húzott c1, c2, r érintő szakaszokkal is kifejezhető, és így a követelmény
2c1+2c2+2r=2k,
ahol c1 és c2 a hegyes szögek, r pedig a derékszög csúcsából húzott érintőszakasz hossza. Innen
c1+c2=c=k-r,
esetünkben c=264,0 mm, vagyis csak az átfogó hosszát kell mérnünk. A megoldásként elfogadott α4≈58∘ mellett c4=264,5-öt találtunk.
2. Ismeretes, hogy a háromszög területét a kerületnek és a beírt kör sugarának fél-szorzata is megadja, és hogy a körre nézve is t=r2π=2rπ⋅ ⋅r/2. Eszerint mindegyik megoldásunkban a háromszög és a beírt kör területeinek aránya is 2-vel egyenlő. Valóban, körünk kétszeres területe közelítőleg 2⋅52⋅3,14=157cm2, kapott derékszögű háromszögünk területe a befogókból 14,0⋅22,45/2≈157,2cm2. A talált egyenlő szárú háromszögeink területe pedig, ‐ miután a magasságot 115,0, ill. 243,0 mm-nek mértük:
13,7⋅11,5≈157,5cm2,ill.6,5⋅24,3≈157,9cm2.

3. Számos dolgozat ‐ bár arról a feladatban szó sem volt ‐ szerkesztést kívánt bevinni a megoldásba és ezért az 564. gyakorlatban adott módon szerkesztett egy a kör kerületével közelítőleg egyenlő szakaszt. Erre nem volt szükség; nem a kör kerületét kellett mérni, ennek eredményében semmi új nem várható, hanem a más-más szögek esetében adódó háromszögek kerületét mint a szögek függvényét. Már pedig ha szögmérőt használunk, eljárásunk nem tekinthető eukleidészi szerkesztésnek.
4. Trigonometriai ismeretek alapján a szögeket közelítőleg ki is lehet számítani.