Kezdőlap


Feladat:	607. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dringó László
Füzet:	1960/november, 140 - 142. oldal		PDF \| MathML
Témakör(ök):	Indirekt bizonyítási mód, Deltoidok, Érintőnégyszögek, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/december: 607. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés: Csak konvex érintőnégyszögekkel foglalkozunk.

I. megoldás: Minden (konvex) deltoid (és természetesen speciális esetei, rombusz és négyzet is) érintőnégyszög, és átlói merőlegesek egymásra. Ennélfogva, ha az

A B C D

négyszög

A B

B C

C D

D A

oldalainak hossza rendre

a

b

c

d

, akkor a követelmények teljesüléséhez elegendő feltétel a következő:

a = b

c = d

, vagyis hogy az oldalak közül 2‐2 szomszédos pár egyenlő legyen. Megmutatjuk, hogy e feltétel szükséges is, ugyanis az ezzel ellentétes állítás ellentmondásra vezet.
Ha egy érintőnégyszög egy pár szomszédos oldala egyenlő, pl.

a = b

, akkor az ismert szükséges és elegendő

\begin{matrix} a + c = b + d \end{matrix}

(1)

feltételből

c = d

következik, vagyis hogy a további két oldal is egyenlő. Ezért fenti állításunk ellentéte az, hogy van olyan

A B C D

érintőnégyszög, amelyben bármelyik két szomszédos oldal különböző és az átlók merőlegesek. Válasszuk a betűzést úgy, hogy

a < b

és

a < d

legyen. Ekkor

B

-nek az

A C

átlóra való

B'

tükörképe az

M D

szakaszra esik, ahol

M

az átlók metszéspontja, mert

M B = \sqrt[]{A B^{2} - M A^{2}} < \sqrt[]{A D^{2} - M A^{2}} = M D

. Hasonlóan

A

-nak

B D

-re való

A'

tükörképe

M C

-nek belső pontja, így

C B' M ∢ > A' B' M ∢ = A B' M ∢

, és ezért

C B' D ∢ < A B' D ∢

. Mérjük rá az

A B = A B'

szakaszt

B'

-től

B' C

-re és legyen végpontja

E

. Így az

E B' D

és

A B' D

háromszögek két-két oldala egyenlő, ezek közbezárt szöge az előbbiben kisebb, ezért a vele szemben levő oldal is kisebb:

D E < D A = d

. Másrészt

C E = C B' - B' E = b - a

, tehát a

C D E

háromszögben

\begin{matrix} C D < C E + D E < C E + D A, \end{matrix}

vagyis

c < b - a + d

, amiből

a + c < b + d

.
Ez pedig valóban ellentétben áll (1)-gyel. Ezzel a bizonyítást befejeztük.

Valamennyi dolgozat számítás útján adta meg a keresett feltételt. Ilyen megoldás a következő.

II. megoldás: Legyenek a fenti jelölésekkel az átlók metszetei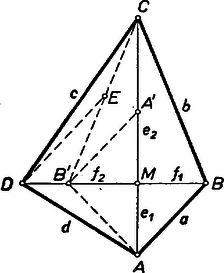

M A = e_{1}

M C = e_{2}

M B = f_{1}

M D = f_{2}

Az átlók merőlegessége folytán

\begin{matrix} a^{2} = e_{1}^{2} + f_{1}^{2}, b^{2} = f_{1}^{2} + e_{2}^{2}, c^{2} = e_{2}^{2} + f_{2}^{2}, d^{2} = f_{2}^{2} + e_{1}^{2}, \end{matrix}

és ebből

\begin{matrix} a^{2} - d^{2} = f_{1}^{2} - f_{2}^{2} = b^{2} - c^{2} \end{matrix}

(2)

Másrészt (1)-ből

\begin{matrix} a - d = b - c . \end{matrix}

(3)

(2) és (3) teljesülnek egyrészt, ha mindkét oldaluk 0, vagyis

a = d

és

b = c

. Másrészt, ha (3) egyik oldala sem 0, akkor a (2) átalakításával adódó

\begin{matrix} (a - d) (a + d) = (b - c) (b + c) \end{matrix}

egyenlőségnek (3)-mal való osztásából

\begin{matrix} a + d = b + c, \end{matrix}

(4)

ez pedig (3)-mal összeadva

a = b

, továbbá

d = c

-re vezet. Mindkét lehetőségben a négyszög 2‐2 szomszédos oldala egyenlő. Ez velejáró következménye ‐ szükséges feltétele annak, hogy az érintőnégyszög átlói merőlegesek legyenek. Ekkor a négyszög deltoid.
E feltétel elegendő is, mert pl.

a = b

és

c = d

folytán

a + c = b + d

, és így a deltoid érintőnégyszög, másrészt ismeretes, hogy átlói merőlegesek.

Dringó László (Budapest, Fazekas M. g. II. o. t.)

Megjegyzések. 1. A (2) egyenlőségből így is haladhatunk tovább. Átrendezéssel

\begin{matrix} a^{2} + c^{2} = b^{2} + d^{2} . \end{matrix}

(5)

Ezt (1) négyzetéből levonva

\begin{matrix} {(a + c)}^{2} - (a^{2} + c^{2}) = {(b + d)}^{2} - (b^{2} + d^{2}), \end{matrix}

vagyis

\begin{matrix} 2 a c = 2 b d . \end{matrix}

(6)

És ezt (5)-ből levonva, átalakítással

\begin{matrix} {(a - c)}^{2} = {(b - d)}^{2} \end{matrix}

és mivel a betűzés megváltoztatásával mindig elérhetjük, hogy

a \geq c

és

b \geq d

, azért

\begin{matrix} a - c = b - d, \end{matrix}

ami azonos (4)-gyel. Így (1), (4) és (6) szerint merőleges átlópárral bíró érintőnégyszögben a szemben fekvő oldalpárok összege is, különbsége is és szorzata is egyenlő.
2. Akik ismerik a hiperbolának ezt a meghatározását: azon pontok mértani helye, melyekre nézve a két adott ponttól (a fókuszoktól) mért távolságok különbsége adott állandó, és pedig kisebb az adott pontok távolságánál, ‐ és szemléletes képük is van a hiperboláról, hogy ti. a fókuszokat összekötő egyenesre (a hiperbola egyik tengelyére), merőleges egyenesnek legfeljebb két közös pontjuk van a hiperbolával, éspedig ha kettő van, azok a tengelyre tükrös párt alkotnak, ‐ azok a fenti deltoidfeltétel szükséges voltát szemlélet alapján a következőkből is beláthatják. Ha

A B C D

érintőnégyszög, akkor (1)-ből

a - b = d - c = 2 e

, tehát

B

és

D

annak a hiperbolának pontjai, melynek fókuszai

A

és

C

, és állandó különbsége

2 e

. Ha pedig

A C ⊥ B D

, akkor

B

és

D

A C

-re tükrös pontpár. ‐ Ez a ,,belátás'' azonban nem bizonyítás !