Kezdőlap


Feladat:	604. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Kiss Tünde , Kopcsányi Zsuzsa , Kóta József , Porpáczy Erzsébet
Füzet:	1960/november, 137 - 138. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/december: 604. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az állítás bizonyítására elég megmutatnunk, hogy a $B D E$ háromszög két szöge, éspedig a $D$ és $E$ -nél levők, egyenlők. Valóban a csúcsszögek egyenlősége, az $A C D$ és $A B E$ háromszögek szögeinek összege, valamint a feltevések alapján

\begin{matrix} E D B ∢ = A D C ∢ = 180^{\circ} - A C D ∢ - C A D ∢ = 180^{\circ} - A B E ∢ - B A E ∢ = \\ = B E A ∢ = B E D ∢ . \end{matrix}

A bebizonyított tétel szerint

B E = B D = d

. Ennek alapján

c

és

d

-ből megszerkesztjük az

A B E

derékszögű háromszöget, ennek

A E

átfogóján a

B

körül

d

sugárral írt körrel kimetsszük

D

-t, végül az

A B

átmérő fölötti

k

Thalész-kör és a

B D

egyenes második metszéspontjában megkapjuk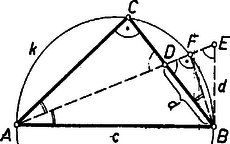

C

-t.

A B C

háromszög megfelel a követelménynek, ugyanis derékszögű, és benne az

A E \equiv A D

egyenes felezi a

B A C

szöget, mert

\begin{matrix} B A E ∢ = 90^{\circ} - B E D ∢ = 90^{\circ} - B D E ∢ = 90^{\circ} - C D A ∢ = C A D ∢ . \end{matrix}

D

akkor adódik az

A E

szakaszon, ha

d < c

. Ez a szerkeszthetőség egyetlen feltétele.

Porpáczy Erzsébet (Jászberény, lg. I. o. t.)

Megjegyzés: Az

A B E

háromszög megszerkesztése után

C

-t a

k

-ból az

A B

egyenesnek

A E

-re való tükörképével is kimetszhetjük. Ekkor

B A E ∢ = E A C ∢

, és az

A B C

háromszög megfelelő voltának bizonyításához azt kell megmutatnunk, hogy teljesül a

B D = d

követelmény, ami éppen a feladat állítása. A

B A C

szög akkor adódik hegyes szögnek, ha fele, a

B A E

szög kisebb

45^{\circ}

-nál, ennek feltétele, hogy

d < c

legyen, mert így az

A B E

derékszögű háromszögben

A

-nál kisebb szög adódik, mint

E

-nél.

Kopcsányi Zsuzsa (Budapest, Berzsenyi D. lg. II. o. t.)

II. megoldás: Megmutatjuk, hogy a

B D E

háromszögben a

B F

szögfelező (

F

A D

egyenesen) egyben magasság is; ebből már következik a bizonyítandó állítás. Valóban, a

C B E

és

C A B

szögek egyenlők, mert mindkettő pótszöge a

C B A

szögnek, így a felezésükkel kapott

C B F = D B F

és

C A D

szögek is egyenlők. Egyenlők továbbá a

B D F

és

A D C

szögek is, mert csúcsszögek. Így a

B F D

és

A C D

háromszögek harmadik szögei is egyenlők:

B F D ∢ = A C D ∢ =

derékszög, állításunknak megfelelően. Eszerint

F

rajta van

k

-n.
Fordítva: a

B

-ből az

A D

szögfelezőre bocsátott

B F

merőleges felezi a

D B E = C B E

szöget, mert az egyenlő szárú háromszög szárszögének felezője azonos az ugyanazon csúcsból húzott magassággal. De közvetlenül is belátható: így ugyanis

F

szerkesztésnél fogva

k

-n van és felezi a

C B

ívet:

\hat{C F} = \hat{F B}

, mert a

B A F

és

C A F

szögek egyenlők. Ezért az ezen íveken fekvő

C B F

és

F B E

kerületi szögek egyenlők.
Ennek alapján az I. megoldásbeli szerkesztés helyességét így igazolhatjuk.

B E

k

-nak érintője, ezért a

B A D = B A F

szög (ahol most

F

A E

és

k

metszéspontja) egyenlő a

B F

íven fekvő

F B E

,,húr-érintő'' szöggel. Ez segédtételünk megfordítása szerint egyenlő az

F B D = F B C

szöggel, az utóbbi pedig az ugyancsak az

F C

íven fekvő

F A C = D A C

szöggel.

Kiss Tünde (Tamási, Béri Balogh Á. g. II. o. t.)

III. megoldás: Az állítást a szögfelező osztási arányáról ismert tételből kiindulva is bizonyíthatjuk. Eszerint

\begin{matrix} B D : C D = B A : C A . \end{matrix}

Másrészt a felezés és a merőleges szerkesztés folytán a

B E A

és

C D A

derékszögű háromszögek hasonlók, ezért

\begin{matrix} B E : C D = B A : C A . \end{matrix}

E két aránypár második arányai azonosak, ezért az első arányok is egyenlők:

\begin{matrix} B D : C D = B E : C D . \end{matrix}

Ha pedig két egyenlő értékű arány utótagjai egyenlők, akkor az előtagok is egyenlők:

B D = B E

Kóta József (Tatabánya, Árpád g. II. o. t.)