Feladat: 599. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Gáspár Rezső 
Füzet: 1960/szeptember, 24 - 25. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Érintőnégyszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1959/november: 599. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 583. gyakorlat I. megoldásában* más jelölésekkel minden húrnégyszögre megmutattuk, hogy az átlók metszéspontjának az oldalakon való vetületei érintőnégyszöget adnak, egyben azt is láttuk, hogy a beírt kör középpontja azonos az átlók metszéspontjával. Így csak azt kell megmutatnunk, hogy PQRS húrnégyszög.

 
 

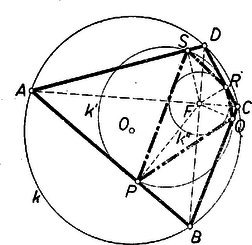
F-nek bármelyik két szomszédos oldalra való vetülete a kérdéses oldalak közös végpontjával és F-fel együtt húrnégyszöget alkot. Ennek alapján ábránk jelöléseivel a PQRS négyszög P csúcsánál fekvő szög két részére, az említett bizonyításhoz hasonlóan
FPQ∢=FBQ∢≡DBC∢=DAC∢≡SAF∢=SPF∢,
és így
SPQ∢=2FPQ∢=2DBC∢=2FBC∢.

Hasonlóan adódik, hogy SRQ∢=2ACB∢=2FCB∢. Ennélfogva a PQRS négyszög szemben fekvő P és R csúcsainál fekvő szögek összege, a háromszög külső szögének tételét az FBC háromszögre alkalmazva
SPQ∢+SRQ∢=2(FBC∢+FCB∢)=2AFB∢.
Ez feltevésnél fogva 180∘-kal egyenlő, tehát a PQRS négyszög húrnégyszög.
 

Gáspár Rezső (Debrecen, Kossuth L. gyak. g. II. o. t.)
 

Megjegyzés. Az 583. gyakorlat 3. ábráján bemutatotthoz hasonló eset itt nem fordulhat elő, mert mint a megoldáshoz hasonlóan könnyen meg lehet mutatni, az átlók merőlegessége folytán a körülírt körnek az oldalak által lemetszett íveire AB^+CD^=AD^+BC^, így egyik ív sem haladhatja meg a 180∘-ot, a körülírt kör középpontja mindig belső pontja az ABCD négyszögnek.
*XX. kötet 130. o. (1960. április).