Feladat: 596. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Fazekas Patrik ,  Góth László ,  Kóta József ,  Kunszt Zoltán ,  Molnár Mária ,  Nováky Béla 
Füzet: 1960/október, 66 - 72. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Kombinatorikus geometria térben, Gyakorlat
Hivatkozás(ok):Feladatok: 1959/november: 596. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. 1. A követelménynek megfelelő pontok együtteseit röviden pontrendszereknek, a háromszögekben a szárak közös végpontját főcsúcsnak fogjuk nevezni. Síkbeli, 5 pontból álló rendszer gyanánt megfelelnek (1. ábra):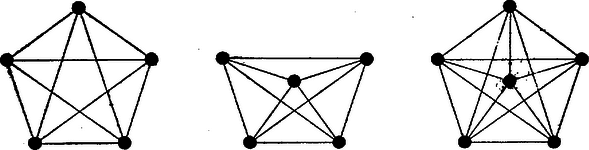
a) egy szabályos ötszög csúcsai,
b) egy szabályos ötszög középpontja és négy csúcsa.

 
 

I. 1. a.       I.1.b.       I.2.
 
1. ábra
 

2. Síkbeli, 6 pontból álló rendszer: egy szabályos ötszög középpontja és valamennyi csúcsa.
A követelmény teljesülését elég a 2. rendszerre bizonyítani, mert az 1. a) és 1. b) rendszerek a 2.-ból egy-egy pont elhagyásával is kiadódnak. Az pedig nyilvánvaló, hogy ha egy pontrendszerre a követelmény teljesül, akkor a belőle egy vagy több pont elhagyása után visszamaradt pontok közül is ‐ hacsak legalább 3 pont marad vissza ‐ bármely 3 pont egyenlő szárú háromszöget alkot, hiszen a visszamaradó rendszer bármely három pontja beletartozik az eredeti rendszerbe. ‐ Ha már most a 2. elhelyezésből kiválasztott három pont tartalmazza a középpontot, akkor a háromszög két oldala az ötszög k körülírt körének sugara, és így egyenlők. Ha pedig mindhárom pont ötszögcsúcs, akkor azok k kerületét úgy osztják három ívre, hogy ezek hosszúságainak aránya vagy 1:1:3 ‐ ha ti. az ötszög egymás utáni 3 csúcsát választjuk ‐ vagy 1:2:2 ‐ ha ti. az előbbi ponthármas egyik szélső pontját az utána következő ötszögcsúccsal pótoljuk. Mindkét esetben van két egyenlő ív, ezért a megfelelő két húr is egyenlő, ezek a szárak.
3. Térbeli megoldások előkészítése céljára adunk néhány példát síkbeli, 4 pontból álló rendszerekre (2. ábra).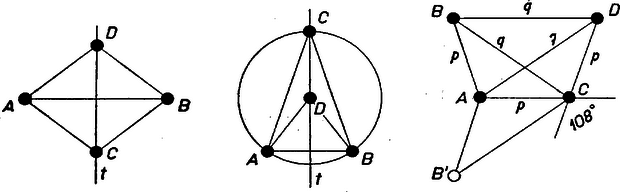
 
 

I. 3. a.       I.3.b.       I.3.c.
 
2. ábra
 

a) Egy tetszés szerinti rombusz 4 csúcsa; más szóval: az A és B pontokhoz hozzávesszük az AB szakasz felező merőlegesének egy tetszés szerinti (de a szakasz felezőpontjától különböző) D pontját és ennek AB-re való C tükörképét (,,tükrös pontpár''-lehetőség).
b) Egy olyan deltoid 4 csúcsa, melyben a szimmetriatengelybe eső átló egyenlő az egyik oldallal; más szóval: az előbbi A, B, D-hez t-nek azt a C pontját vesszük hozzá, amelyet a D körül DA sugárral írt kör metsz ki belőle; még másképpen: az ABC egyenlő szárú háromszög csúcsaihoz hozzávesszük a köréje írható kör D középpontját (,,kör''-lehetőség, ábránk nem konvex deltoidot mutat).
c) Egy szabályos ötszög 4 csúcsa.
Az a) és b) rendszerekben általában 3-féle szakaszhosszúság fordul elő, éspedig az egyenlő szakaszok száma 4, 1, 1, ill. 3, 2, 1. Lehetséges azonban további egyenlőség, ilyenkor a rendszer háromszögei között van egyenlőoldalú. A szabályos háromszög 3-féleképpen tekinthető egyenlő szárúnak, így minden szabályos háromszög révén a rendszer főcsúcsainak száma 2-vel emelkedik. Az a)-ban CD=AC esetén ACD és BCD szabályosak, igy ACB∢=120∘, tehát AB>AC, a hatodik szakasz hosszabb, a főcsúcsok száma ilyenkor 8 (I. 3. a'); ugyanerre jutunk b)-ből AC=AD-vel. b)-ből AB=AD-vel, valamint AB=AC-vel 1 ‐ 1 szabályos háromszöge lesz a rendszernek: ABD, ill. ABC, így a főcsúcsok száma 6 (I. 3b' és b'').
II. A feladat térben való megoldásán azt értjük, hogy a kijelölt pontok nem lehetnek egy síkban. Előző észrevételünk alapján itt előbb 7 pontból álló rendszereket sorolunk fel, az ezekből 1, ill. 2 pont elhagyásával visszamaradó rendszerek 6, ill. 5 pontra térbeli megoldások, hacsaknem egy síkban vannak. Néhány 7 pontból álló rendszer (3. ábra):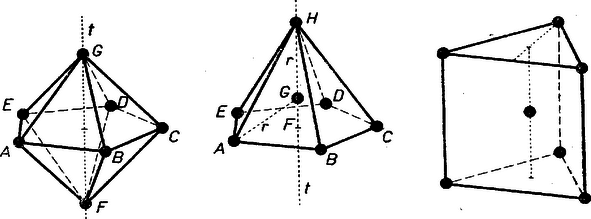
 
 

II. 1. a.       II.1.b.       II.1.c.
 
3. ábra
 

1. a) A fenti I. 1.a) rendszer, kiegészítve a középpontban az ötszög S síkjára merőlegesen álló t egyenesnek ‐ az ötszög térbeli tengelyének ‐ két az S-re tükrös F, G pontjával.
b) Az I. 1. a)-hoz 6-iknak t tetszés szerinti G pontját vesszük, 7-iknek pedig t-ből az egyik olyan H-t, amelyet a G körül GA sugárral írt gömb metsz ki. Más szóval: a t-n választott H-val kiegészített I. 1. a) rendszerhez hozzávesszük körülírt gömbjének G középpontját (,,gömb''-lehetőség, megfelel a fenti kör-lehetőségnek). G gyanánt az ötszög F középpontját is vehetjük, így az előálló ,,gúla'' magassága egyenlő az alap köré írt kör sugarával.
c) Egy 3 oldalú, egyenlő élű egyenes hasáb 6 csúcsa és a köréje írható gömb középpontja.
2. Két az előzőkből elhagyással ki nem adódó, 6 pontból álló rendszer (4. ábra):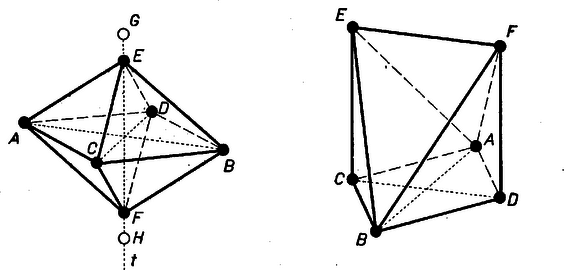
 
 

II. 2. a.          II.2.b.
 
4. ábra
 

a) Az I. 3. a) rendszert (a fenti mintára vett) térbeli tengelyének azokkal az E, F pontjaival egészítjük ki, amelyekre EA=FA=AC (,,alapél-oldalél''-lehetőség). Így C, E, D, F egy négyzet csúcsai. (Ugyanilyet ad t-nek az a G, H pontpárja, amelyre GC=HC=AC, vagy ha egy négyzet csúcsaihoz hozzácsatoljuk tengelyének egy tükrös pontpárját.) Ha ACBD egyenlő átlójú rombusz (vagyis négyzet), akkor mindkét módon a szabályos oktaéder csúcsainak rendszerét kapjuk.
b) Egy 60∘-os hegyesszögű ACBD=R rombusz rövidebb CD átlójának végpontjaiban R síkjára állított merőlegeseken, e sík ugyanazon oldalán úgy vesszük fel E, F-et, hogy EC=FD=CD (vagyis CDFE négyzet).
3. Két az előzőkből általában ki nem adódó 5 pontból álló rendszer: a), b). Egy egyenlő szárú háromszög csúcsait kiegészítjük a tükrös pontpár, ill. a gömb-(speciálisan a sugár-magasság) lehetőséggel. (Ilyen rendszer marad vissza a II. I. a) és b)-ből ‐ 3. ábra ‐ pl. C és E elhagyásával és az ABD háromszöget úgy megváltoztatva, hogy ne legyen 36∘-os szöge.)
A fentiekkel mindegyik kívánt pontrendszerre adtunk példát.
Könnyű bizonyítani, hogy a felsorolt pontrendszerek bármely 3 pontja egyenlő szárú háromszöget alkot. Ezt az I. 3. és a további rendszerekre itt helyszűke miatt az olvasóra bízzuk; hangsúlyozzuk azonban, hogy elvben bármely állítás csak bizonyítással együtt fogadható el. Számos dolgozat e tekintetben hiányos.
Megjegyezzük végül, hogy mivel minden esetben van megoldás csupa valóságos háromszögekkel, azért elfajult háromszögeket (egy egyenesbe eső 3 pontot) tartalmazó rendszereket nem tekintettünk megoldásnak.
Összeállítva kiegészítésekkel a következők dolgozataiból:
 

Fazekas Patrik (Mosonmagyaróvár, Kossuth Lajos g. I. o. t.)

Góth László (Budapest, Könyves Kálmán g. II. o. t.)

Kóta József (Tatabánya, Árpád g. II. o. t.)

Kunszt Zoltán (Pápa, Türr István g. II. o. t.)

Molnár Mária (Sztálinváros, Kerpely A. kohóip. t. II. o. t.)

Nováky Béla (Budapest, I. István g. II. o. t.)

 

Megjegyzés: Néhányan ‐ elsősorban a fentiek ‐ igyekeztek azt megmutatni, hogy 5 pont síkban való megfelelő elhelyezésére nincs más lehetőség, mint az I. 1. a) és b) rendszer, 6 pontra pedig csak az I. 2. rendszer. Az állítás igaz, de a bizonyítás senkinél sem teljes. Egyébként a feladat nem kívánta ezt a vizsgálatot. Alább a fenti dolgozatokból vett gondolatokkal és kiegészítésekkel megmutatjuk, hogy 4 pont megfelelő síkbeli elhelyezésére az I. 3. a)‐c) rendszerek az összes megoldást adják (az egyenlő oldalú háromszögeket tartalmazó I. 3. a') és b'), b'')-vel együtt), majd vázoljuk a továbbhaladást 5 pont esetében. A főcsúcsot a betűjele fölé tett vonallal jelöljük, pl. A¯BC jelentése: AB=AC (de ez nem zárja ki BC=AB lehetőségét).
Keressük meg először az olyan 4 tagú rendszereket, melyekben mindegyik pont csak egy háromszögnek főcsúcsa; így mind a 4 pont egyszer főcsúcs, mert a rendszernek 4 háromszöge van. Legyen az egyik háromszög A¯BC. Ennek BC alapja a BCD háromszögben vagy alap, akkor BCD¯, vagy szár, és pl. B a főcsúcs: B¯CD, így két folytatás veendő figyelembe. Az első esetben ABD főcsúcsa már csak B lehet: AB¯D, és hasonlóan AC¯D. E háromszögekből rendre BA=AC, CD=DB, DB=BA, tehát a BACD négyszög rombusz, és ebből következik a negyedik háromszögből adódó AC=CD egyenlőség is. Vagyis ilyen rendszer egyedül az I. 3. a).
A második esetben A¯BC és B¯CD egyértelmű folytatása ABD¯ és AC¯D (2. ábra, I. 3. c), tehát AB=AC=CD=p és BC=BD=AD=q. Így az A¯BC és C¯AD háromszögek egybevágók, mert oldalaik hossza p, p, q, továbbá B¯CD és D¯BA egybevágók, mert oldalaik p, q, q. Az A¯BC, C¯AD háromszög-pár közös AC oldalegyenese nem választhatja szét a nem közös B, D csúcsokat, mert szétválasztás esetén a BAC, ill. DCA szögek váltószögek lennének, így AB#CD állna, a 4 pont paralelogrammát alkotna AC és BD átlókkal. Ez pedig lehetetlen, mert minden paralelogrammában az átlók négyzetösszege egyenlő az oldalak négyzetösszegével1 és ez itt p2+q2=2(p2+q2)-re vezetne. Így B, D az AC-nek csak egy oldalán lehetnek. Könnyű belátni, hogy BD∥AC és így pontjaink egy szimmetrikus trapéz csúcsai. Nem lehet p=q, mert így a 4 ponttal meghatározott 6 szakasz mindegyike egyenlő volna, holott 5 szakasz egyenlőségéből adódik, hogy a pontok egy 60∘-os szögű rombusz csúcsai, így pedig a 6-ik szakasz, az egyik átló, hosszabb. Ezért feltehetjük, hogy p<q. Ekkor a trapéz körüljárása ABDC, és BAC=α tompaszög, továbbá a fentiekből CAD∢=90∘-α/2, és BAD∢=ABD∢=180∘-α. Ezekből az A-nál levő szögekre (180∘-α)+(90∘-α/2)=α, tehát α=108∘; megkaptuk az I. 3. c) rendszert.
Hátra vannak az olyan rendszerek, amelyekben van olyan pont, amely legalább két háromszögben főcsúcs. Az ilyen pont egy harmadik háromszögben is főcsúcs, mert pl. D¯AB és D¯AC azt jelenti, hogy DA=DB=DC, így A, B, C egy D középpontú körön vannak, fennáll tehát D¯BC. Eszerint az I. 3. b) rendszerrel állunk szemben.
Hasonlóan két olyan pontot feltéve, amely több háromszögnek főcsúcsa ‐I. 3. a')-re jutunk. Ha pedig a háromszoros főcsúcson túl egynél több egyszeres főcsúcs létezését tesszük fel, akkor I. 3. b') és b'') adódik ki. További eset nem lehetséges, mert egy pont nem lehet mindnégy háromszög főcsúcsa, hiszen mindegyik pont 3 háromszögben szerepel; másrészt valamennyi I. 3. rendszert megkaptuk.
Most már az 5 pontból álló rendszerek kifejlesztése lehetséges a 4 pontból állókból, 1 további alkalmas pont hozzávételével. E célra összegyűjtjük annak összes lehetőségeit, ahogyan egy egyenlő szárú háromszöget 4 pontból álló rendszerré lehet kiegészíteni. Minden kapott 4-tagúból 4 ilyet olvashatunk le (rendre a négy csúcsot újnak tekintve), de több ismétlődés van. A lehetőségek a következők:
α) Az egyik alapcsúcs tükrözése a másik szár felező merőlegesén; ez azonban csak akkor használható, ha a főcsúcsnál levő szög 36∘, vagy 108∘ I. 3. c).
β) Egyik alapcsúcs tükrözése a másik száron, pl. B az ACD¯ háromszög A csúcsából az I. 3. b) rendszerekben. (A tükörkép rajta van a főcsúcs körül a szárral mint sugárral írt körön. A főcsúcsnál levő φ szög nem lehet derékszög, mert így a tükörkép a tükrözött szár meghosszabbításába esnék, 3 pont egy egyenesen lenne.)
γ) A főcsúcs tükrözése az alapon, pl. az I. 3. a)-ban A¯CD és A-ból B.
δ) A körülirt kör középpontjának hozzávétele, pl. az I. 3. b)-ben ABC¯-ből D.
ε) A szimmetriatengely azon pontjának hozzávétele, amelyet a főcsúcs körül a szárral mint sugárral irt kör metsz ki, éspedig az alapnak a főcsúccsal ε1) egyező, ill. ε2) ellentétes partján (I. 3. b-ben C, az ábrán ε1).
Ezek alapján 5-tagú rendszert 3 tagúból egy csapásra is képezhetünk: fenti lehetőségeink közül kettőt választva egyszerre két, D és E pontot kapcsolunk A¯BC-hez, ‐ ezáltal DAB, DAC, DBC és EAB, EAC, EBC máris egyenlő szárúak ‐, majd megvizsgáljuk, hogy D és E együtt bármelyik eredeti csúccsal egyenlő szárú háromszöget adnak-e. Pl. α és α-val a főcsúcsnál 36∘ vagy 108∘ szögű háromszöget mindkét szár felező merőlegesén tükrözve I. 1. a)-t kapjuk; ugyanebből α és δ-val I. 1. b)-t. Mivel azonban a γ)-ε) lehetőségek egy a t tengelyből való pontot csatolnak a meglevőkhöz, és t-ben az eredeti főcsúcs is benne van, azért az új 2 pont közül csak egyik képezhető a γ)-ε) lehetőségek szerint. Más szóval általában legalább egyik új pont β) szerint képezendő. β-ban viszont a tükrözési szár kétféleképpen választható.
Példaképpen keressünk olyan rendszert, amely A¯BC-hez D-t is, E-t is a β lehetőséggel képezi. Így B, C, D, E az A körüli AB sugarú körön vannak, ezért fennáll A¯DE, másrészt D és E az A¯BC tengelyére tükrösek, ezért áll BDEΔ≃CDEΔ, tehát elég pl. BDE egyenlő szárú voltát biztosítani a BAC=φ szög alkalmas megválasztásával. Ezt φ nagysága szerint 4 esetben vizsgáljuk.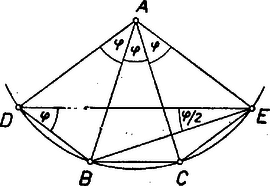
 
 
5. ábra
 

1. AD-t AB-n át AE-be 3φ nagyságú forgás viszi. Ha ez kisebb 180∘-nál (5. ábra), vagyis DE elválasztja A-t B-től, akkor BDE nem lehet egyenlő szárú, mert B-nél levő szöge (360∘-3φ)/2, ami tompaszög, a D és E-nél levő szögek pedig különbözők: φ≠φ/2.
2. Ha 2φ<180∘<3φ, vagyis 90∘>φ>60∘, akkor A és B a DE-nek egy oldalán vannak. A szögek előbbi kifejezéseivel az egyenlő szárúság beáll, ha B∢=D∢, amiből φ=72∘ és megkapjuk I. 1. b)-t, vagy ha B∢=E∢, ebből azonban a β) lehetőségben kizárt φ=90∘ adódik.
3. A 2φ>180∘ és 3φ≤360∘, vagyis 90∘<φ≤120∘ esetben D∢>90∘, E∢>45∘ és B∢<45∘, nincs megoldás.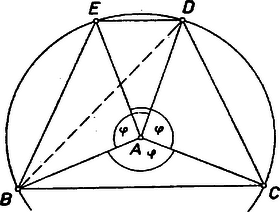
 
 
6. ábra
 

4. Ha 3φ>360∘, akkor az AD-t AE-be átvivő kisebb forgás 3φ-360∘ (6. ábra), a B szög ennek fele, BDE∢=BAE∢/2=180∘-φ és a BED szög fele a nagyobb BAD szögnek, vagyis 180∘-φ/2. Itt B∢=D∢-ből φ=144∘, ami ismét I. 1. b)-re vezet, más megoldás nincs. Ezzel a példát befejeztük.
Olyan rendszer sincs, amelyben D-t a β, E-t a γ lehetőséggel képeznők. Így ugyanis D és E a BC-nek ellentett oldalán vannak (7. ábra), mert 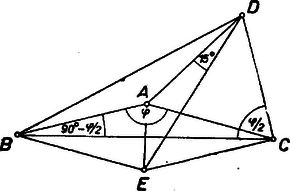ABC∢<90∘ folytán DBC∢<180∘.
 
 
7. ábra
 

Így a DCE szög összeadással adódik DCB és BCE-ből és értéke 90∘. Ezért kell, hogy C¯DE álljon, így ACD egyenlő oldalú és φ=30∘, vagy 150∘. Ebből pedig a DEA háromszög szögei 105∘, 30∘, 45∘, ill. 15∘, 30∘, 135∘, tehát ez nem egyenlő szárú. ‐ Sokban hasonlít ehhez a β-δ pár vizsgálata. ‐ Ha a további lehetőségek valamely párja pontrendszert ad, az azonos I. 1. a) vagy I. 1. b)-vel, tehát nincs más 5-tagú síkbeli pontrendszer.
1Lásd pl. az 1006. feladat megoldását a XXI. kötet 1. számban, 20. o.