Kezdőlap


Feladat:	583. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dobó Ferenc , Góth László , Nováky Béla
Füzet:	1960/április, 130 - 132. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Húrnégyszögek, Érintőnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/szeptember: 583. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek az $E$ -ből az oldalakra bocsátott merőlegesek talppontjai rendre $K_{1}, L_{1}, M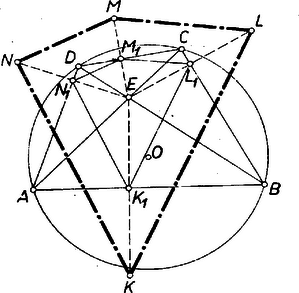_{1}, N_{1}$ (1. ábra).

1. ábra

Ezek felezik az

E K, E L, E M, E N

szakaszokat, ezért a

K_{1}, L_{1}, M_{1}, N_{1} = Q_{1}

négyszög hasonló helyzetű

K L M N = Q

-hoz, a hasonlóság középpontja

E

, aránya

1 : 2

. Elég tehát az állítás igazolásául

Q_{1}

-ről megmutatni, hogy érintőnégyszög és érintő körének középpontja

E

, akkor ugyanez áll

Q

-ra is, mert

E

a hasonlósági transzformációban önmagának a megfelelője.

Q_{1}

érintőnégyszög, mert szögeit

E K_{1}, E L_{1}, E M_{1}, E N_{1}

rendre felezik. Elég ezt pl.

E K_{1}

-re és az

L_{1}, K_{1}, N_{1}

szögre belátni, mert

Q

-nak egyetlen oldala, csúcsa sincs kitüntetve, ezért

Q_{1}

-nek sem, és így bizonyításunk

Q_{1}

bármelyik szögére érvényes.

E N_{1} A K_{1}

és

E L_{1} B K_{1}

húrnégyszögek, mert szemközti

N_{1}

és

K_{1}

ill.

L_{1}

, és

K_{1}

csúcsuknál fekvő szögeik derékszögek. Ezért a

Q_{1}

-ben a

K_{1}

-nél fekvő szög két része a kerületi szögek tétele alapján

\begin{matrix} ε_{1} = E K_{1} N_{1} ∢ = E A N_{1} ∢ = C A D ∢, \\ ε_{2} = E K_{1} L_{1} ∢ = E B L_{1} ∢ = D B C ∢, \end{matrix}

(felhasználtuk, hogy

E

mindkét átlón rajta van és hogy

N_{1}, L_{1}

, az

A D

, ill.

B C

oldalon van). Az utóbbi szögek az

A B C D

négyszög köré írt körnek az

A, B

csúcsokat nem tartalmazó

C D

ívén nyugvó kerületi szögek, ezért egyenlők, tehát

ε_{1} = ε_{2}

. Ez az, amit bizonyítani akartunk.

Nováky Béla (Budapest, I. István g. II. o. t.)

Megjegyzés. Lényegében ugyanezek felhasználásával magára

Q

-ra is bizonyíthatjuk az állítást, pl. hogy

E K

felezi

Q

-nak

L K N

szögét. A tükrözés folytán

A N = A E = A K

, ezért az

N K E

háromszög körülírt körének középpontja

A

, és hasonlóan a

K L E

háromszögé

B

. Másrészt

A D

, ill.

B C

A E N

, ill.

B E L

háromszögnek szimmetriatengelye, tehát felezi

A

, ill.

B

-nél fekvő szögüket. Így a kerületi és középponti szögek tétele alapján

\begin{matrix} \underset{̲}{E K N} ∢ = E A N ∢ / 2 = E A D ∢ = C A D ∢ = C B D ∢ = C B E ∢ = \\ = L B E ∢ / 2 = \underset{̲}{L K E} ∢ . \end{matrix}

Állításunkat az egyenlőségsorozat szélső tagjainak összekapcsolása bizonyítja.

Dobó Ferenc (Budapest, Apáczai Csere J. gyak. g. I. o. t.)

II. megoldás: Az előbbi megjegyzésben szereplő, továbbá az

L M E

M N E

háromszögek köré írt

C

, ill.

D

középpontú körök felhasználásával megmutatjuk, hogy

Q

szemben fekvő oldalpárjainak összege ugyanakkora, ebből pedig, mint ismeretes, következik, hogy

Q

érintőnégyszög.

2. ábra

A K N, O B D

és

C L M

háromszögek (2. ábra) hasonlók (

O

az eredeti kör középpontja), mert

A

-ból,

O

-ból, ill.

C

-ből kiinduló oldalaik egyenlők, és a köztük fekvő szög

2 α

(ill.

360^{\circ} - 2 α

, ha

α

tompaszög). Ebből

\begin{matrix} K N : A N = B D : O D = L M : C M \end{matrix}

és tekintettel az

A N = A E

C M = C E

egyenlőségekre

\begin{matrix} K N = \frac{B D}{O D} \cdot A E, L M = \frac{B D}{O D} \cdot C E, \\ és így K N + L M = \frac{B D}{O D} (A E + C E) = \frac{B D \cdot A C}{O D} . \end{matrix}

Ugyanígy a

B L K

O C A

D M N

hasonló (a csúcsoknál

2 β

, ill.

360^{\circ} - 2 β

szögű) egyenlő szárú háromszögekből

\begin{matrix} K L : B K = A C : O A = M N : D N, \end{matrix}

és mivel

B K = B E

D N = D E

és

O A = O D

, azért

\begin{matrix} K L = \frac{A C}{O A} \cdot B E, M N = \frac{A C}{O A} \cdot D E, \\ és így K L + M N = \frac{A C}{O A} (B E + D E) = \frac{A C \cdot B D}{O D} . \end{matrix}

Ezzel állításunkat igazoltuk.

Megjegyzés. Egyetlen dolgozat: Góth Lászlóé (Budapest, Könyves Kálmán g. II. o. t.) mutatott rá arra, hogy ha az

A B C D

négyszög nem foglalja magában körülírt körének

O

középpontját, akkor a

K L M N

négyszög nem konvex, illetőleg háromszöggé fajul el, ha

O

pl. az

C D

oldalra esik. A bebizonyított tények ekkor is helytállók, van olyan kör, amely

K L M N

mindegyik oldalának egyenesét érinti, valamint az átellenes oldalpárok összege is egyenlő.

3. ábra

3.ábránk felvételén az I. megoldás

E N_{1} A K_{1}

és

E L_{1} B K_{1}

húrnégyszögeiben

N_{1}

és

K_{1}

valamint

L_{1}

és

K_{1}

nem szemközti csúcsok (ill. akkor szemköztiek, ha e négyszögeket hurkoltaknak tekintjük) másrészt

N_{1}, L_{1}

A D

, ill.

B C

oldal meghosszabbításán van, ezért a következő számítás helyes:

\begin{matrix} ε_{1} = E K_{1} N_{1} ∢ = 180^{\circ} - E A N_{1} ∢ = C A D ∢, \\ ε_{2} = E K_{1} L_{1} ∢ = 180^{\circ} - E B L_{1} ∢ = D B C ∢ . \end{matrix}

A 4. ábrán a

C A D

és

C B D

szögek derékszögek, ezért

N_{1}

A

-ba,

L_{1}

B

-be esik, így

N_{1}, K_{1}, L_{1}

A B

egyenesre esnek és így

N

K

L

is egy egyenes pontjai.

4. ábra

Ez is mutatja, milyen helytelen az az általános szokás, hogy a vizsgálódáshoz egyetlen ábrát vesznek alapul és azon is kerülik a ,,szokatlanságokat''.