| Feladat: | 582. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Füzet: | 1960/április, 129 - 130. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Sokszög lefedések, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1959/szeptember: 582. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A ,,The Mathematical Gazette'' (London) szöveg nélküli ábrái alapján. 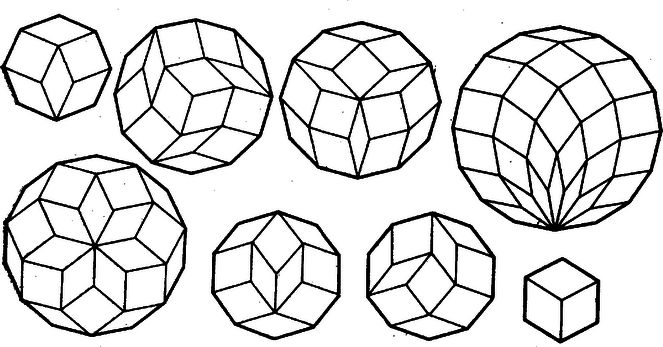 Ábránk mindegyik sokszög lefedésére mutat legalább egy lehetőséget. Nyilvánvaló, hogy a hatszögre ez az egyetlen. Hogy az nyolcszög is csak a mutatott módon fedhető le, az a következőképpen látható be. Lefedésben mindegyik oldalához teljes oldalával támaszkodik egy-egy rombusz. minden szöge , egyenlő az ferde rombuszok tompaszögével. Ezért ha egy támaszkodik egy oldalához, akkor ennek egyik szomszédjához is, ennélfogva -nek páros számú oldalához támaszkodik . Lehetetlen azonban, hogy mind a 8 oldalhoz támaszkodjék, mert így minden -et elhelyezünk, minden második csúcsánál -os szögek maradnak szabadon és ezek nem fedhetők le egyrétűen a hátralevő derékszögű rombuszokkal (négyzetekkel). Így ugyancsak pozitiv páros számú oldalhoz kell -nek támaszkodnia. Ez a szám csak 2 lehet, mert mindkét az -nek csak 1 ‐ 1 oldalához támaszkodhat. Már most a két nem csatlakozhat -nek sem szomszédos, sem egymásra merőlegesen álló oldalaihoz, mert így átfedés állna elő, és szemközti oldalakhoz sem, mert akkor köztük a kerület mindkét szabadon maradó szakaszát 3 egymás utáni -oldal alkotná, vagyis páratlan számú oldal, holott az -ek beillesztéséhez páros számú egymás utáni oldalra van szükség. Így a két csak úgy támaszkodhat két -oldalhoz, hogy a még fedetlen 6 oldal 4 és 2-tagú összefüggő szakaszokat alkosson. Ezekhez a 2, ill. 1 csak egyféleképpen támaszkodhat, és az ezek után fedetlenül maradt rész éppen egy -fel egybevágó. Nem sok rendszeres kísérlettel meg lehet állapítani, hogy a 10-szögnek 7, ill. a tengelyes szimmetriát mutatókat azonosaknak tekintve 6 különböző lefedése lehetséges, ezekből egy egytengelyű és egy aszimmetrikus megoldást mutatunk be. Hogy az egyre nagyobb és nagyobb oldalszámú sokszögek lefedésére a lehetőségek száma mind nagyobb, ezt az állítást valószínűvé teszi, hogy a lefedésekben egyre többször adódnak olyan 6-, 8-, 10- -szög alakú részletek, amelyeknek szemben fekvő oldalai párhuzamosak és egyenlők, tehát egy középpontra tükrösek, az ilyenek pedig legalább még egy módon lefedhetők. A 12-szögre mutatott példáinknak 3-as forgási szimmetriájuk van, és a másodiknak 3 tengelye is. |