Feladat: 581. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bácskai Ferenc ,  Góth László 
Füzet: 1960/április, 127 - 129. oldal  PDF  |  MathML 
Témakör(ök): Eltolás, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1959/szeptember: 581. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tegyük fel, hogy az adott szögek közül α kisebb: α<γ, továbbá, hogy a vizsgálandó fb és fd szögfelezők a négyszög belsejében metszik egymást, metszéspontjuk E (1. ábr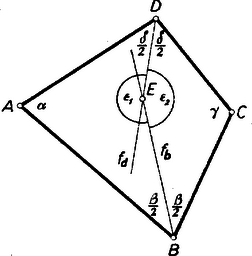a).

 
 
1. ábra
 

Így a BE,DE szakaszok az ABCD négyszöget az EDAB és EDCB négyszögekre vágják szét. Az E csúcsnál az EDAB négyszögben ε1=360∘-α-(β+δ)/2 nagyságú szög van, az EDCB-ben pedig ε2=360∘-γ-(β+δ)/2 nagyságú. Ezek csak az α, ill. γ kivonandóban térnek el, így a feltevésnél fogva ε1>ε2. Másrészt ε1+ε2=360∘, tehát ε1>180∘, ε2<180∘, vagyis ε1 az E pontnál keletkező négy szög közül háromnak az összegét adja, ε2 pedig egy olyan szög nagyságát, amelynek terében nincs félegyenese a szögfelezőknek.
Megmutatjuk, hogy ε2 tompaszög, így a szögfelezők előírt hegyes szögeként kiegészítő szöge, ζ=180∘-ε2 veendő. Ugyanis β+δ=360∘-(α+γ) alapján
ε2=360∘-γ-β+δ2=360∘-γ-180∘+α+γ2=180∘-γ-α2.
Négyszögünk konvexsége folytán γ és α kisebbek 180∘-nál, ugyanez áll különbségükre, így annak fele, ε2 utolsó alakjának kivonandója kisebb 90∘-nál, ennélfogva ε2 valóban nagyobb 90∘-nál. Eszerint a kérdéses hegyes szög: ζ=(γ-α)/2.
Az olyan eseteket, amelyekben fb és fd-nek E metszéspontja a négyszög kerületére, vagy a négyszögön kívülre esik, visszavezetjük a már vizsgált esetre. A négyszög kerületére csak úgy eshet E, ha vagy B-be, vagy D-be esik, mert a BA,BC egyeneseken fb-nek nincs más pontja, mint B, a DA, DC egyeneseken pedig fd-nek nincs más pontja, mint D. Legyen E a B-ben, ill. fb-nek kifelé való meghosszabbításán (2. ábra).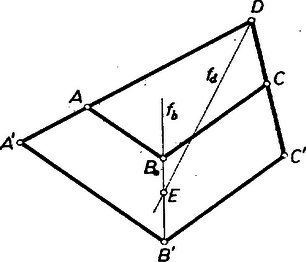
 
 
2. ábra
 

Ekkor az fb-nek a négyszögből kilépő meghosszabbításán, E-n túl felvett B' ponton át BA,BC-vel párhuzamost húzva, és ezeknek DA,DC-vel való metszéspontját A',C'-vel jelölve az A'B'C'D' négyszög B' és D-nél fekvő szögeinek felezői fb és fd, és ezek az új négyszögön belül metszik egymást. Ezért fenti eredményünk szerint ζ=(γ'-α')/2 és ez egyenlő (γ-α)/2-vel, mert az A'B'C'D és ABCD négyszögek egymás utáni szögei egyállásúak, és ezért egyenlők.
A kérdéses szög nem létezik, ha fb és fd párhuzamosok vagy egybeesők. Ez csak akkor áll fenn, ha α=γ. Messe ugyanis fb,fd az AD, ill. BC egyenest D', ill. B'-ben (3. áb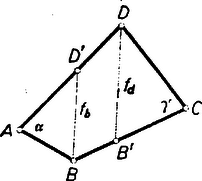ra).
 
 
3. ábra
 

fb és fd azonossága esetén D'≡D,B'≡B és az ABCD négyszög deltoid, mert a felezések folytán BA és BC, valamint DA és DC egymás tükrös párjai fb-re, és ezért α=γ. Különben pedig CB'D∢=CBD'∢=β/2 és AD'B∢=ADB'∢=δ/2, mert egyállású szögek, vagyis a B'CD és BAD' háromszögek 2 ‐ 2 szöge egyenlő, ezért harmadik szögeik is, amint állítottuk. Fordítva, α=δ-ból következik, hogy fb és fd egybeesők vagy párhuzamosak. ‐ A kapott feltétel ellentétben áll a fenti ζ megállapításában felhasznált α<γ feltevéssel, ezért a nyert ζ érték itt nem használható. De a fenti értéknek α=γ esetére való felhasználása sem vezet hibára, mert ζ=0∘-ot ad, amit úgysem fogadunk el két egyenes hajlásszögének.
 

Góth László (Budapest, Könyves Kálmán g. II. o. t.)

 

II. megoldás: Nincs szükség eseteknek E helyzete szerinti megkülönböztetésére, ha a szöget nem kötjük helyhez, hanem csupán irányok közti elfordulásnak tekintjük. Toljuk el a CB,CD félegyeneseket C-pontnál fogva A-ba, új helyzetük AB'(||CB) A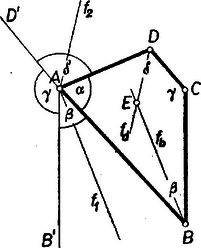D'(||CD; 4. ábra).
 
 
4. ábra
 

Ekkor az (egyenes szögnél kisebb) B'AD' szög a BCD=γ szöggel egyenlő, mert egyállásúak, és BAB' az ABC=β-val, DAD' az ADC=δ-val egyeulő, mert váltószögek, tehát az A pontnál megjelent négyszögünknek mind a négy szöge. Legyen továbbá f1,f2 az fb,fd szögfelezőkkel az A-n át húzott párhuzamosoknak az a félegyenese, amely az egyenes szögnél kisebb B'AB, ill. DAD' szög terében fekszik. Az fb és fd közti, keresett szögek egyenlők az f1 és f2 közti szögekkel. Ez utóbbiak pedig felezik a B'AB, DAD' szöget, mert pl. f1 és AB szöge váltószöge fb és BA szögének, amely β/2-vel egyenlő. Már most f1-ből f2-be átfordulva egyik irányban ϑ1=β/+α+δ/2=α+(β+δ)/2 szög van, a másik irányban ϑ2=β/2+γ+δ/2=γ+(β+δ)/2. Továbbá α=γ esetén ϑ1=ϑ2=360∘/2=180∘, vagyis f1 és f2 egymás meghosszabbításai, tehát fb, fd párhuzamosak, vagy egybeesők, α<γ esetén pedig ϑ1<ϑ2 tehát f1 és f2-nek ϑ1 a szokásos értelemben vett hajlásszöge. Ez (α+β+δ)/2+α/2=180∘-γ/2+α/2 alakban is írható, és arról a fentiek szerint látjuk be, hogy tompaszög, számunkra kiegészítő szöge veendő, ζ=180∘-ϑ1=(γ-α)/2.
 

Bácskai Ferenc (Kecskemét, Piarista g. II. o. t.)

 

Megjegyzés. Teljeseknek csak azokat a dolgozatokat fogadtuk el, amelyekben legalább utalás van arra, hogy a szögfelezők a négyszögön kívül is metszhetik egymást, vagy arra, hogy α és γ nagyságviszonya hogyan befolyásolja a végeredményt. Amely dolgozatok egyik kérdést sem érintették, azokat hiányosaknak minősítettük.