| Feladat: | 575. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Kovács Imre , Rátkai János , Somlai Klára , Veres Gyula , Zalán Péter | ||
| Füzet: | 1959/december, 176 - 178. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Pont körüli forgatás, Háromszögek nevezetes tételei, Szögfüggvények, síkgeometriai számítások, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1959/május: 575. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Legyenek az háromszög () oldalaira befelé rajzolt szabályos háromszögek csúcsai , , , és tegyük fel, hogy ezek égy egyenesbe esnek. , és a tengelyére szimmetrikus párok, ezért vagy merőleges a tengelyre, vagy egybeesik vele. Az utóbbi esetben , így -nél -os, és -nél -os szög van.1 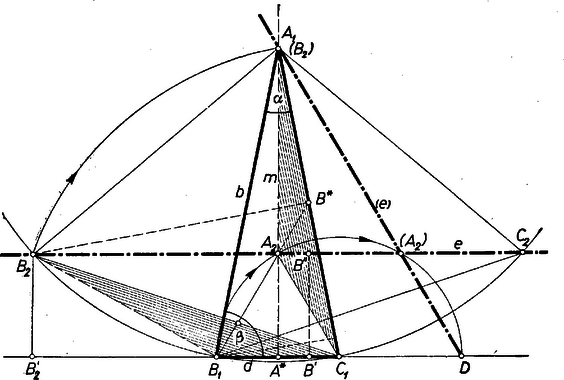 A másik esetben párhuzamos a alappal, ezért és -nek fölötti magassága egyenlő. Ekkor , , , , az körül sugárral írt körön vannak, így az kerületi szög -os, mert fele a -os középponti szögnek. Másrészt a szög -os, mert váltószögként egyenlő az szöggel; így az háromszög derékszögű, és -re képezett tükörképével szabályos háromszöget alkot, tehát (ahol ). Legyen és vetülete a egyenesen , ill. , így a derékszögű háromszögben , , tehát . Most már az derékszögű háromszögből a szokásos jelölésekkel , és négyjegyű táblázatból , .
Megjegyzések. 1. Az háromszög szögeit más kiindulásból is meghatározhatjuk. A háromszög egybevágó az háromszöggel, mert körül -os forgatással egymásba vihetők át. Így , és . Lényegében így állította elő alakját szerkesztéssel Katona Mária (Budapest, Szilágyi E. gyak lg. I. o. t.): a szabályos háromszög révén kitűzte a egyenest, ennek körül -kal elforgatott helyzetéből felező merőlegesével kimetszette -et (az ábrán elforgatott helyzetét (), ill. () jelöli). Szerkesztése számítással folytatható: az elforgatott egyenes a alapú szabályos háromszög szára, így és , . 2. Számítással is beláthatjuk, hogy . Ugyanis az egyenlő szárú háromszögben -nél , ezért -nél szög van, másrészt , így összeadással .
3. A , , szögekkel bíró háromszögben nincs érdekessége annak, hogy a három ‐ azaz két ‐ csúcspont egy egyenesre esik. Ez az ,,elfajult'' és a következő ,,igazi'' megoldás Lőrincz Pálnak idevágó tárgyú cikkében2 is együtt lép fel, közös vonásuk, hogy az háromszög területe 0. ‐ Az igazi megoldás -ja egyenlő a cikk -ével, mert -ben , ezért a -re merőleges magassága terület kétféle kifejezése: alapján: és így . II. megoldás: Legyen felezőpontja , ennek vetülete -en ; továbbá vetülete -n (a szakaszon, mert ,3 hegyesszög). Ekkor , itt az , és derékszögű háromszögek hasonlósága alapján , másrészt , tehát a fenti egyenletből , és innen , .
Megjegyzések. 1. Mindjárt az indulásnál szögfüggvényeket használva -ből , és figyelembevételével . (Ugyanis csak mellett lehetnek -nek az -vel és -gyel egyező partján, tehát )
2. Összehasonlítás céljából vázolunk egy nehéz úton járó megoldást is: Az háromszög derékszögű. Vegyük a fenti -t 1-nek és számítsuk ki -t. Így , ; a pythagorászi egyenlőségből két, alkalmas rendezés utáni négyzetreemeléssel és -ra tekintettel , (a fenti megoldás) és (idegen gyök).
3. A II. megoldás módján helyett bármely hegyes szöggel megoldhatjuk a feladatot. magassága általában: Másrészt a egybeesés mindig esetén áll be, pl. -kal mellett. Ezek szerint -kal mindkét megoldás szabályos háromszög. 4. Egy-két dolgozat elég pontos rajzról észrevette, hogy , , egy egyenesen vannak, vagy hogy és harmadolják egymást. Ez helyes, a fentiek alapján könnyen belátható, de hibás az, ha ilyen észrevételeket bizonyítás nélkül egy ,,megoldás'' alapjává kívánunk tenni. 1Lásd az 549. gyakorlat 1. ábráját a novemberi számban 131. o.2Lőrincz Pál: Megjegyzések egy versenyfeladathoz, KML. XVII. kötet, 129-134. o., közelebbről 132 o. (1958. december).3 Az ábrán a szakasz pótlandó. |