| Feladat: | 573. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bácsy Zs. , Biborka T. , Bollobás Béla , Dóra Gy. , Endreffy Z. , Faludi Irén , Farkas Z. , Fekete Béla , Fekete J. , Fischer A. , Fritz J. , Gagyi Pálffy A. , Gálfi l. , Gáti P. , Grüner Gy. , Hegedűs J. , Juhász I. , Katona Mária , Kéry G. , Klimó J. , Kóta G. , Kóta J. , Kovács Imre , Krámli A. , Máté A. , Máté E. , Molnár E. , Opálény M. , Pósa L. , Rády Erika , Székely J. , Szoboszlai L. | ||
| Füzet: | 1960/február, 64 - 65. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb sokszögek hasonlósága, Eltolás, Diszkusszió, Négyszögek szerkesztése, Körérintési szerkesztések, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1959/május: 573. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Tekintsük a feladatot megoldottnak és legyen a keresett , kör középpontja , (a -t -nak középpontjával összekötő egyenesen, ill. az -re -ban emelt merőlegesen) és közös sugaruk . A két kör ‐ sugaraik egyenlősége folytán ‐ csak külső érintkezésben lehet egymással, ezért . 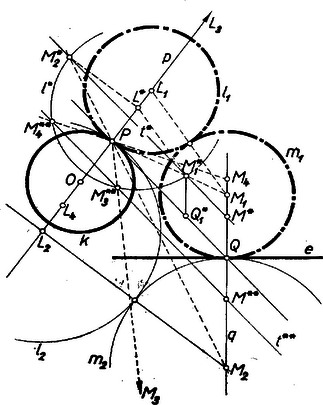 Így a négyszögben ismerjük a oldalt, a és -nál fekvő szögeket és a többi három oldal arányát: . A szögek és az arány alapján e négyszöghöz szerkeszthetünk hasonlót, úgy hogy -re -től és -ra -tól felmérjük a tetszés szerinti szakaszt, az -on át -val húzott párhuzamost elmetsszük az körül sugárral írt -körrel, a kapott metszésponton át párhuzamost húzunk -val, és vesszük ennek -val való metszéspontját. Így a négyszög hasonló helyzetű -hez, ennélfogva -et -ból -gyel metszhetjük ki, -et pedig -ből a -gal -n át húzott párhuzamossal. Valóban, a és , valamint a és háromszögpárok hasonlóságából , ezért folytán ; másrészt , így a és háromszögek hasonlók, és folytán , tehát az , pontok körül sugárral írt , körök érintik egymást, továbbá a -n, ill. -n át -re, -ra merőleges egyenest és evvel -t, ill. -t. és kölcsönös helyzete szerint -ként pontot és ugyanennyi megoldást kapunk. és egyikének irányát ellentétesre fordítva ugyanezen eljárással ismét legfeljebb 2 megoldás adódik, így a megfelelő körpárok száma általában legfeljebb 4. (Az ábrán , a megfelelő -ből adódó , középpontok is fel vannak tüntetve.) Könnyen belátható, hogy ha és párhuzamosak, akkor a megoldások száma 3. Nincs megoldás, vagy végtelen sok megoldás van, ha és egybeesnek, aszerint, hogy metszi -t vagy érinti.
Megjegyzés. A szerkesztés végrehajtásában -et mellőzhetjük, mert (a bizonyítás szerint) az -gal -en át húzott párhuzamossal is kimetszhető, vagy kitűzhető alapján, figyelembe véve, hogy iránya aszerint egyező, ill. ellentétes -éval, amint és irányai megegyeznek, ill. ellentétesek. II. megoldás: Legyen a kör -beli érintőjének -vel való metszéspontja , a keresett körök érintkezési pontja (az első körpárra) és -nek a körökkel való második metszéspontja ; ekkor a sugarak egyenlősége folytán . 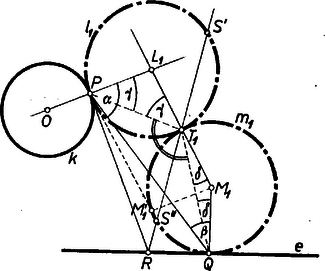 Az -ből húzott érintőkre és szelőkre (a 2. ábrán látható helyzetben) , hasonlóan . Ezekből , és ez számára mértani helyként egy körüli kört jelöl ki, melynek sugara egyenlő annak a négyzetnek az oldalával, amelyet az oldalakkal szerkesztett téglalap köré irható körbe írtunk. Így a sugár nagyságra és közé esik, és egyike -on belül van, a másika kívül, esetén pedig mindkettő a -on. Még egy mértani helyet ad -nak -ből vett látószöge. A 2. ábra helyzetében és jelöléseivel egyrészt a háromszögből , másrészt , és e két kifejezésből kiküszöbölésével és jelöléssel . (A különbségek képezésében támaszkodtunk az ábrára, hogy ti. , a , ill. -nak a használt félegyenesén vannak; így a egyenesnek csak egyik partján lehet, ennek megfelelően -nak két nyílású látószögköríve közül csak az ezen a parton fekvő veendő figyelembe. Hasonlóan az 1. ábrán vázolt további megoldásokra , , .) A két mértani hely metszéspontja adja a keresett körpár érintkezési pontját ( és -nak -hoz képest elfoglalt helyzete folytán csak egy pontban metszheti -t), a középpontokat pedig felező merőlegese metszi ki -ból. III. megoldás: Toljuk el -et irányában és nagyságával; az előálló az körön van (2.ábra). Az egyenlő szárú háromszög alakja megszerkeszthető, mert szárainak iránya és , így megkapjuk oldalainak arányát és a alap irányát. Másrészt . Ezek szerint -re , ezért rajta van egyrészt a alappontokkal és a szerkeszthető aránymutatóval meghatározott Apollóniosz-körön, másrészt a -n átmenő, megszerkeszthető irányú félegyenesen, tehát megszerkeszthető. Most már sorra megkapjuk -et, -et és ezekből -et.
|