Kezdőlap


Feladat:	565. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kéki Zsuzsanna , Kóta József , Sebestyén Zoltán
Füzet:	1960/január, 10 - 11. oldal		PDF \| MathML
Témakör(ök):	Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/április: 565. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek az $r$ sugarú, $O$ középpontú kör $P$ belső pontján átmenő, egymásra merőleges húrok 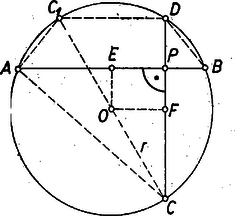$A B$ és $C D$ .

A szeletek

S

négyzetösszege alkalmas zárójelbefoglalással

S = (A P^{2} + C P^{2}) + (B P^{2} + D P^{2}) = A C^{2} + B D^{2}

. Megmutatjuk, hogy a

C

-hez tartozó átmérő másik végpontját

C_{1}

-gyel jelölve

A C_{1} = B D

, így az

A C C_{1}

derékszögű háromszögre Pythagorász tételét alkalmazva

S = A C^{2} + A C_{1}^{2} = C C_{1}^{2} = 4 r^{2}

, állandó.
Valóban, a feltevés, valamint Thalész tétele folytán

A B

és

D C_{1}

merőlegesek

C D

-re, így

D C_{1}

párhuzamos

A B

-vel. Eszerint

A

B

D

és

C_{1}

egy körbeírt, tehát szimmetrikus trapéz csúcsai, és ebben a kérdéses

A C_{1}

és

B D

vagy a két szár, vagy a két átló szerepét játsszák, mindenképpen egyenlők. ‐ Ha

P

felezi

A B

-t, akkor

C D

A B

-re merőleges átmérő,

C_{1} \equiv D

és

A C_{1} = A D = B D

azért teljesül, mert az

A B D

háromszög egyenlő szárú.
A tétel más fogalmazása pl. az, ha kimondjuk a kérdéses összeg értékét: a szeletek négyzetösszege egyenlő az átmérő négyzetével. Vagy, a használt átalakításra tekintettel, ‐ amely helyett

S = A D^{2} + B C^{2}

-et is írhattunk volna ‐: merőleges átlójú, húrnégyszög két-két szemközti oldalának négyzetösszegei egyenlők a körülírt kör átmérőjének négyzetével.

Sebestyén Zoltán (Celldömölk, Berzsenyi D. g. I. o. t.)

Megjegyzés. Nem használtuk ki, hogy

P

a körön belül van, ezért az állítás minden olyan külső

P

pontra is érvényes, amelyen át lehet

k

-t metsző merőleges szelőpárt fektetni, vagyis amelyből

k

a derékszögnél nagyobb szögben látható, másképpen, amely közelebb van

O

-hoz, mint a

k

-ba írható négyzet oldala.

II. megoldás: Legyen

O

-nak

A B

-n, ill.

C D

-n levő vetülete, vagyis e húrok felezőpontja

E

F

. Feltehetjük (alkalmas betűzéssel elérhetjük), hogy

P

D F

szakaszon, esetleg

F

-ben van. Így

O E = F P = C P - C F = C P - (C P +

+ D P) / 2 = (C P - D P) / 2

, másrészt

A E = (A P + B P) / 2

, és ezekkel az

O A E

háromszögből Pythagorász tételével

\begin{matrix} A E^{2} + O E^{2} = r^{2}, {(A P + B P)}^{2} + {(C P - D P)}^{2} = 4 r^{2}, \\ (A P^{2} + B P^{2} + C P^{2} + D P^{2}) + 2 (A P \cdot B P - C P \cdot D P) = 4 r^{2} . \end{matrix}

Itt a második zárójelbeli különbség tagjai az egymást metsző húrok szakaszaira ismert tétel szerint egyenlők, a különbség

0

, és így a kérdéses négyzetösszeg

4 r^{2}

-tel egyenlő, függetlenül

P

helyzetétől, amit bizonyítanunk kellett.

Kóta József (Tatabánya, Árpád g. I. o. t.)

Megjegyzés. Az utóbbi megoldásnak kissé más alakja az, ha

r

O E

O F

-fel kifejezzük a két húr felét és a szeleteket, és így képezzük

S

-et; összevonások után

4 r^{2}

-et kapunk.

Kéki Zsuzsanna (Mezőtúr, Teleki Blanka lg. II. o. t.)